Окресность

Окре́стность точки — множество, содержащее данную точку, и близкие к ней.

Определения

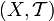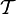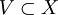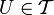• Пусть задано топологическое пространство $(X,\mathcal{T})$, где X — произвольное множество, а $\mathcal{T}$ — определённая на X топология. Множество $V \subset X$ называется окрестностью точки $x\in X$, если существует открытое множество $U\in \mathcal{T}$ такое, что $x \in U \subset V$.

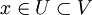• Аналогично окрестностью множества 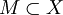$M \subset X$ называется такое множество 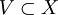$V \subset X$, что существует открытое множество 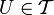$U\in \mathcal{T}$, для которого выполнено $M \subset U \subset V$.

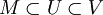Замечания

• Приведённые выше определения не требуют, чтобы окрестность V была открытым множеством, но лишь чтобы она содержала открытое множество U. Некоторые авторы настаивают на том, что любая окрестность открыта. Тогда окрестностью множества называется любое содержащее его открытое множество. Это не принципиальное для развития дальнейшей топологической теории различие. Однако, в каждом случае важно фиксировать терминологию.

• Прямо из определения следует, что V является окрестностью множества M тогда и только тогда, когда V есть окрестность любой точки $x\in M$.

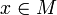Проколотая окрестность

Множество 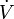$\dot{V}$ называется проко́лотой окре́стностью (вы́колотой окрестностью) точки $x\in X$, если

$\dot{V} = V \setminus \{x\},$

где V — окрестность x.

Строго говоря, проколотая окрестность не является окрестностью в смысле данного выше определения.

Пример

Пусть дана вещественная прямая со стандартной топологией. Тогда [ − 1,2] является окрестностью, а ( − 1,2) — открытой окрестностью точки 0. Множество 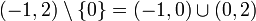$(-1,2) \setminus \{0\} = (-1,0) \cup (0,2)$ является проколотой окрестностью 0.

См. также

• ε-окрестность.