Неравенство Рао-Крамера

В математической статистике неравенством Краме́ра — Ра́о (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая её через информацию Фишера.

Формулировка

Пусть дана статистическая модель 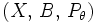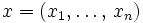$(X,\,B,\,P_\theta)$, $x = (x_1,\dots,\,x_n)$ — выборка размера n, определена функция правдоподобия 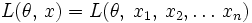$L(\theta,\,x) = L(\theta,\;x_1,\,x_2,\dots\,x_n)$ и выполнены следующие условия (условия регулярности):

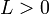• $L_{}^{} > 0$ и везде дифференцируема по $\theta_{}^{}$.
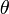• Функция $U(\theta,\,x) = \frac{\partial \ln L(\theta,\,x)}{\partial \theta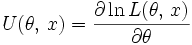}$ (функция вклада выборки) имеет конечную дисперсию (или, что то же, конечна информация Фишера).
• Для любой статистики 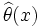$\widehat{\theta}(x)$ имеет место равенство

$\frac{\partial}{\partial \theta} \int\limits_X \widehat{\theta}(x)\, L(\theta,\,x)\, dx = \int\limits_X \widehat{\theta}(x)\, \frac{\partial}{\partial \theta} L(\theta,\,x)\, dx$.

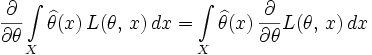Пусть при этих условиях дана статистика 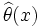$\widehat{\theta}(x)$, которая оценивает дифференцируемую функцию τ(θ), причём смещение $\mathrm{M}_\theta \widehat{\theta}(x) - \tau(\theta)$ равно дифференцируемой функции b(θ). Тогда справедливы следующие утверждения:

• $\mathrm{D}_\theta \big(\widehat{\theta}(x) - \tau(\theta) - b(\theta)\big)\geqslant\frac{\big(\tau'(\theta) + b'(\theta)\big)^2}{I_n(\theta)}$;
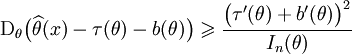• равенство достигается тогда и только тогда, когда 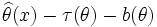$\widehat{\theta}(x) - \tau(\theta) - b(\theta)$ представляется в виде $a(\theta) U(\theta,\,x)$.

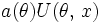Здесь 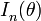$I_n^{}(\theta)$ — информация Фишера.

Частный случай

Часто используется следующая, более слабая версия неравенства. Пусть выполнены условия регулярности, а 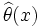$\widehat{\theta}(x)$ — несмещённая оценка параметра θ. Тогда неравенство выглядит так:

$\mathrm{D}_\theta\,\widehat{\theta}(x)\geqslant\frac{1}{I_n(\theta)}$.

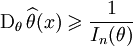Этот случай получается из первого, если взять τ(θ) = θ и b(θ) = 0.

Применение

Оценка параметра называется эффективной, если для неё неравенство Крамера — Рао обращается в равенство. Таким образом, неравенство может быть использовано для доказательства того, что дисперсия данной оценки наименьшая из возможных, то есть что данная оценка в некотором смысле лучше всех остальных.