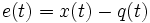- Наблюдатель (теория управления)
-
Система
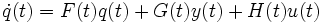 (1)
(1)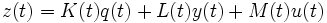 (2)
(2)
является наблюдателем для системы
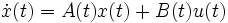 (3),
(3),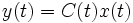 (4),
(4),
если для каждого начального состояния
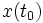 системы (3)-(4) существует начальное состояние
системы (3)-(4) существует начальное состояние 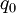 для системы (1)-(2), такое, что равенство
для системы (1)-(2), такое, что равенство 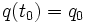 приводит к
приводит к 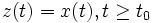 при всех управлениях
при всех управлениях 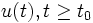 .
.Здесь
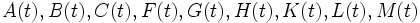 — матрицы соответствующей размерности.
— матрицы соответствующей размерности.Если размерность
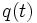 равна размерности
равна размерности 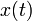 и выполнение условия
и выполнение условия 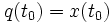 дает
дает 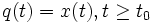 при всех управлениях
при всех управлениях 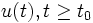 , то система (1) называется наблюдателем полного порядка для системы (3)-(4).
, то система (1) называется наблюдателем полного порядка для системы (3)-(4).Набор дифференциальных уравнений (3) описывает изменение во времени состояния некоторой системы.
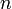 -мерный вектор
-мерный вектор 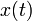 , называемый вектором состояния, описывает состояние этой системы в момент времени
, называемый вектором состояния, описывает состояние этой системы в момент времени 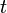 .
.  -мерный вектор
-мерный вектор 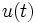 описывает управляющие воздействия на систему и называется вектором управления или просто управлением.
описывает управляющие воздействия на систему и называется вектором управления или просто управлением.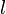 -мерный вектор
-мерный вектор 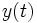 представляет собой линейную комбинацию переменных состояния системы (3), которую мы можем измерить. Обычно
представляет собой линейную комбинацию переменных состояния системы (3), которую мы можем измерить. Обычно 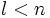 .
. 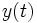 называют наблюдаемой переменной.
называют наблюдаемой переменной.Теорема 1. Система (1) является наблюдателем полного порядка для системы (3)-(4) тогда и только тогда, когда
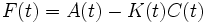 ,
, 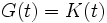 ,
, 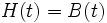 , где
, где 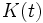 является произвольной переменной во времени матрицей соответствующей размерности. В результате наблюдатели полного порядка имеют следующую структуру:
является произвольной переменной во времени матрицей соответствующей размерности. В результате наблюдатели полного порядка имеют следующую структуру:![\dot q(t)=A(t)q(t)+B(t)u(t)+K(t)[y(t)-C(t)q(t)]](/pictures/wiki/files/49/19a49d96a1a6402fd963eb1438051479.png) (5).
(5).
Матрица
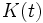 называется матрицей коэффициентов усиления наблюдателя. Наблюдатель полного порядка можно также представить в виде
называется матрицей коэффициентов усиления наблюдателя. Наблюдатель полного порядка можно также представить в виде ![\dot q(t)=[A(t)-K(t)C(t)]q(t)+B(t)u(t)+K(t)y(t)]](/pictures/wiki/files/50/2bcea4e7ecb4fdc71ac74b9c7c850e7b.png) , откуда следует, что устойчивость наблюдателя определяется поведением матрицы
, откуда следует, что устойчивость наблюдателя определяется поведением матрицы 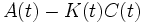 .
.В случае системы с постоянными параметрами, когда все матрицы в постановке задачи являются постоянными, включая матрицу коэффициентов усиления
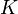 , устойчивость наблюдателя следует из расположения характеристических чисел матрицы
, устойчивость наблюдателя следует из расположения характеристических чисел матрицы 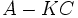 , называемых полюсами наблюдателя. Наблюдатель будет устойчив, если все его полюса расположены в левой половине комплексной плоскости.
, называемых полюсами наблюдателя. Наблюдатель будет устойчив, если все его полюса расположены в левой половине комплексной плоскости.Теорема 2. Рассмотрим наблюдатель полного порядка (5) для системы (3)-(4). Ошибка восстановления
удовлетворяет дифференциальному уравнению
![\dot e(t)=\left[A(t)-K(t)C(t)\right]e(t)](/pictures/wiki/files/101/e7849483beb2ed6fb12e2a02a1986bc5.png) .
.
Ошибка восстановления обладает тем свойством, что
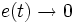 при
при 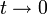
для всех
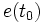 тогда и только тогда, когда наблюдатель является асимптотически устойчивым.
тогда и только тогда, когда наблюдатель является асимптотически устойчивым.Чем дальше в левой половине комплексной полуплоскости удалены полюса наблюдателя, тем быстрее сходится ошибка восстановления к нулю. Это достигается увеличением матрицы коэффициентов усиления
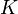 , однако это повышает чувствительность наблюдателя к шумам измерений, которые, возможно, присутствуют в наблюдаемой переменной
, однако это повышает чувствительность наблюдателя к шумам измерений, которые, возможно, присутствуют в наблюдаемой переменной 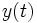 .
.Примечания
См. также
Ссылки
Wikimedia Foundation. 2010.