- Мнимая экспонента
-
Экспоне́нта (комплексного переменного) — функция, задаваемая соотношением f(z) = ez.
Данное определение в целом формально и не имеет достаточной строгости. Поэтому, и в случае со степенной функцией, будем строго определять экспоненту с помощью аналитического продолжения её вещественного аналога. Для начала определим формальное выражение
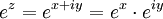 . Ясно, что определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Поэтому для полной корректности построения необходимо доказать аналитичность функции ez.
. Ясно, что определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Поэтому для полной корректности построения необходимо доказать аналитичность функции ez.Для этого разложим её вещественный множитель в ряд:
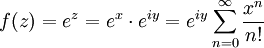
и проверим его сходимость, которая легко доказывается:
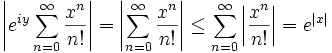 .
.Ряд сходится абсолютно, следовательно, вообще сходится, таким образом, сумма этого ряда в каждой конкретной точке и будет определять значение аналитической функции f(z) = ez. Согласно теореме единственности, полученное продолжение будет единственно, следовательно, теперь эта аналитическая функция определена полностью и однозначно.
Одним из интересных свойств комплексной экспоненты, не проявляющимся в вещественном случае, является её периодичность. Это неудивительно — из формулы Эйлера, которая ранее была формальной, а теперь превратилась в полностью корректное утверждение следует, что
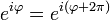 . Отличие её от остальных ранее известных периодических функций — наличие чисто мнимого периода.
. Отличие её от остальных ранее известных периодических функций — наличие чисто мнимого периода.Максимальной областью однолистности экспоненты будет, как следует из её периодичности, горизонтальная полоса на комплексной плоскости
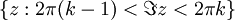
Wikimedia Foundation. 2010.
