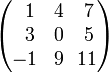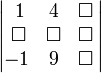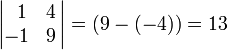- Минор матрицы
-
Минор
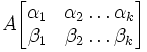 матрицы A ― определитель матрицы, элементы которой стоят в данной прямоугольной матрице порядка k (который называется также порядком этого минора) на пересечении строк с номерами
матрицы A ― определитель матрицы, элементы которой стоят в данной прямоугольной матрице порядка k (который называется также порядком этого минора) на пересечении строк с номерами 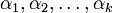 и столбцов с номерами
и столбцов с номерами 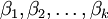 .
.Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
Пример
Например, есть матрица:
Предположим, надо найти дополнительный минор M23. Этот минор - определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:
Получаем M23 = 13
См. также
Wikimedia Foundation. 2010.