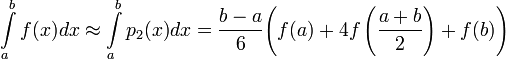Метод Симпсона

Формула Симпсона относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).

Рассмотрим отрезок [a, b]. Пусть известны значения вещественной функции f(x) в точках a, (a+b)/2, b. Существует единственный полином 2-й степени p₂(x), график которого проходит через точки (a, f(a)), ((a+b)/2,f((a+b)/2), (b, f(b)). Формулой Симпсона называется интеграл от этого полинома на отрезке [a, b]:

${\int\limits_a^b f(x) dx} \approx {\int\limits_{a}^{b} {p_2(x)} dx} = \frac{b-a}{6}{ \left( f(a) + 4 f\left(\frac{a+b}{2}\right) + f(b) \right)}$

Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Погрешность при интегрировании по отрезку [a,b] с шагом h определяется по формуле:

$\frac{(b-a)}{180}h^4 M_4$,

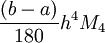где $M_4=\max\limits_{x\in[a,b]} |f^{IV} (t)|$ — максимум четвёртой производной функции.

Так же, при невозможности оценить погрешность с помощью максимума четвертой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:

$\frac{(b-a)}{36}h^3 M_3$,

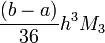где $M_3=\max\limits_{x\in[a,b]} |f^{III} (t)|$ — максимум третьей производной функции.

Ссылки

• Костомаров Д. П., Фаворский А. П. «Вводные лекции по численным методам»