- Формула Симпсона
-
Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).
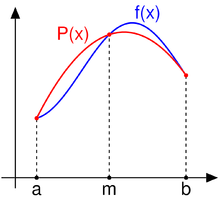
Суть приёма заключается в приближении подынтегральной функции на отрезке
![[a,b]\,\!](8b596d04e319e05cadcc7dcf251a9815.png) интерполяционным многочленом второй степени
интерполяционным многочленом второй степени  , то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.
, то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.Содержание
Формула
Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке
![[a,b]](2c3d331bc98b44e71cb2aae9edadca7e.png) :
:где
 ,
,  и
и  — значения функции в соответствующих точках (на концах отрезка и в его середине).
— значения функции в соответствующих точках (на концах отрезка и в его середине).Погрешность
При условии, что у функции
 на отрезке
на отрезке ![[a,b]](2c3d331bc98b44e71cb2aae9edadca7e.png) существует четвёртая производная, погрешность
существует четвёртая производная, погрешность  , согласно найденной Джузеппе Пеано формуле равна:
, согласно найденной Джузеппе Пеано формуле равна:В связи с тем, что значение
 зачастую неизвестно, для оценки погрешности используется следующее неравенство:
зачастую неизвестно, для оценки погрешности используется следующее неравенство:Представление в виде метода Рунге-Кутты
Формулу Симпсона можно представить в виде таблицы метода Рунге-Кутты следующим образом:
Составная формула (формула Котеса)
Для более точного вычисления интеграла, интервал
![[a,b]](2c3d331bc98b44e71cb2aae9edadca7e.png) разбивают на
разбивают на  отрезков одинаковой длины и применяют формулу Симпсона на каждом из них. Значение исходного интеграла является суммой результатов интегрирования на всех отрезках.
отрезков одинаковой длины и применяют формулу Симпсона на каждом из них. Значение исходного интеграла является суммой результатов интегрирования на всех отрезках.- где
 — величина шага, а
— величина шага, а  — узлы интегрирования, границы элементарных отрезков, на которых применяется формула Симпсона. Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок
— узлы интегрирования, границы элементарных отрезков, на которых применяется формула Симпсона. Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок ![[a,b]\,\!](8b596d04e319e05cadcc7dcf251a9815.png) разбит на
разбит на  узлов) в виде
узлов) в виде 
Также формулу можно записать используя только известные значения функции, то есть значения в узлах:
- где
 означает что индекс меняется от единицы с шагом, равным двум. Следует обратить внимание на удвоение коэффициента перед суммой. Это связано с тем, что в данном случае роль промежуточных узлов играют исходные узлы интегрирования.
означает что индекс меняется от единицы с шагом, равным двум. Следует обратить внимание на удвоение коэффициента перед суммой. Это связано с тем, что в данном случае роль промежуточных узлов играют исходные узлы интегрирования.
Общая погрешность
 при интегрировании по отрезку
при интегрировании по отрезку ![[a,b]\,\!](8b596d04e319e05cadcc7dcf251a9815.png) с шагом
с шагом  (при этом, в частности,
(при этом, в частности,  ,
,  ) определяется по формуле[2]:
) определяется по формуле[2]:![\left| E(f) \right| \leqslant \frac{(b-a)}{2880}h^4 \max\limits_{x\in[a,b]} |f^{(4)} (x)|](73e6b1109d6b857aa9927b327c9c24a0.png) .
.
При невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:
![\left| E(f) \right| \leqslant \frac{(b-a)}{288}h^3 \max\limits_{x\in[a,b]} |f^{(3)} (x)|](1507ec77985211ea89fa8523f247af77.png) .
.
Примечания
- ↑ Формула Ньютона-Симпсона
- ↑ Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. — 4-е изд. — М: БИНОМ, Лаборатория знаний, 2006. — С. 122. — 636 с. — ISBN 5-94774-396-5
Литература
- Костомаров Д. П., Фаворский А. П. «Вводные лекции по численным методам»
- Петров И. Б., Лобанов А. И. Лекции по вычислительной математике
Категория:- Численное интегрирование
Wikimedia Foundation. 2010.


![E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}, \ \ \ \zeta \in [a,b].](e49ee7873cd9c01c2e7e7d781d863728.png)
![\left| E(f) \right| \leqslant \frac{(b-a)^5}{2880} \max\limits_{x\in[a,b]} {\left| f^{(4)}(x) \right|}.](1284336c117479df07733b0aeaf19df6.png)


