- Мера на полукольце
-
Определение. Мерой μ на полукольце ρ называется неотрицательная функция, обладающая свойством аддитивности:
μ(А
 В) = μ(A)+μ(B)
В) = μ(A)+μ(B)для любых А и В, принадлежащих полукольцу ρ и таких, что μ(А
 В)
В) 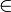 ρ
ρ
Wikimedia Foundation. 2010.
Определение. Мерой μ на полукольце ρ называется неотрицательная функция, обладающая свойством аддитивности:
μ(А В) = μ(A)+μ(B)
В) = μ(A)+μ(B)
для любых А и В, принадлежащих полукольцу ρ и таких, что μ(А  В)
В) 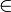 ρ
ρ
Wikimedia Foundation. 2010.
МЕРА — множества, обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в… … Математическая энциклопедия
Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия
ДИСКРЕТНАЯ МЕРА — мера, сосредоточенная на не более чем счетном множестве. Точнее, пусть Xи m меры (вообще говоря, знакопеременные), определенные на одном полукольце множеств (со своим s кольцом измеримых множеств). Мера l наз. дискретной мерой относительно меры m … Математическая энциклопедия
Теорема Каратеодори о продолжении меры — В теории меры теорема Каратеодори утверждает, что произвольная (счётно аддитивная) мера на некотором кольце подмножеств множества может быть продлена на σ кольцо, порожденное кольцом . В случае σ конечности меры такое продолжение является… … Википедия
Гражданская война в Испании — Смерть республиканца анархиста Федерико Боррелла Гарсии (фотография Роберта Капы) … Википедия
РЕГУЛЯРНАЯ ФУНКЦИЯ МНОЖЕСТВА — аддитивная функция m, определенная на системе множеств топологич. пространства, полная вариация к рой удовлетворяет условию где внутренность множества замыкание множества F(E, G, F из области определения m). Ограниченная аддитивная Р. ф. м.,… … Математическая энциклопедия