Фактор-группа

Пусть G — группа, и H — её нормальная подгруппа, то есть для любого элемента 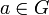$a\in G$ его правый и левый классы смежности совпадают:

aH = Ha

Тогда на классах смежности H в G можно ввести умножение:

(aH)(bH) = abH

Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если aH = a'H и bH = b'H, то abH = a'b'H. Оно определяет структуру группы на множестве классов смежности, а полученная группа называется факторгруппой G по H.

Факторгруппа обозначается G / H.

Свойства

• Теорема о гомоморфизме: Для любого гомоморфизма $\varphi:G\to K$

$G / {\mathrm Ker}\, \varphi \cong \varphi (G)$,

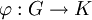
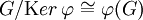то есть фактор группы G по ядру 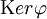${\mathrm Ker} \varphi$ изоморфен её образу 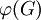$\varphi (G)$ в K.

• Отображение 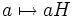$a \mapsto aH$ задаёт естественный гомоморфизм $G \to G/H$.
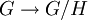• Порядок G / H равен индексу подгруппы [G:H]. В случае конечной группы G он равен | G | / | H | .
• Если G абелева, нильпотентна, разрешима, циклическая или конечнопорождённая, то и G / H будет обладать тем же свойством.
• G / G изоморфна тривиальной группе ({e}), G / e изоморфна G.

Примеры

Пусть 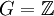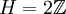$G = \mathbb{Z}$, $H = 2\mathbb{Z}$, тогда G / H изоморфна $\mathbb{Z}_2$.

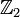Пусть 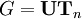$G = \mathbf{UT}_n$ (группа невырожденных верхнетреугольных матриц), 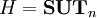$H = \mathbf{SUT}_n$ (группа верхних унитреугольных матриц), тогда G / H изоморфна группе диагональных матриц.

См. также

Для других алгебраических структур, а также множеств, также определены понятия факторов: фактормножество, факторкольцо, факторалгебра, факторполе.

Ссылки

• Винберг Э. Б. Курс алгебры, — М.: Издательство «Факториал Пресс», 2002, ISBN 5-88688-060-7.