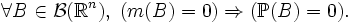- Абсолютно непрерывное распределение
-
Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве
 . В случае когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.
. В случае когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.Содержание
Плотность вероятности
Пусть
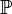 является вероятностной мерой на
является вероятностной мерой на  , то есть определено вероятностное пространство
, то есть определено вероятностное пространство 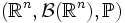 , где
, где 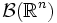 обозначает борелевскую σ-алгебру на
обозначает борелевскую σ-алгебру на  . Пусть m обозначает меру Лебега на
. Пусть m обозначает меру Лебега на  .
.Определение 1. Вероятность
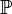 называется абсолютно непрерывной (относительно меры Лебега) (
называется абсолютно непрерывной (относительно меры Лебега) (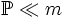 ), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:
), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:Если вероятность
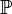 абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция
абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция  такая, что
такая, что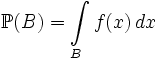 ,
,
где использовано общепринятое сокращение
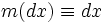 , и интеграл понимается в смысле Лебега.
, и интеграл понимается в смысле Лебега.Определение 2. Функция f, определённая выше, называется производной Радона-Никодима вероятности
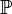 относительно меры m или плотностью вероятности
относительно меры m или плотностью вероятности 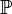 (относительно меры m):
(относительно меры m):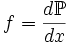 .
.
Свойства плотности вероятности
- Плотность вероятности определена почти всюду. Если f является плотностью вероятности
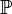 и f(x) = g(x) почти всюду относительно меры Лебега, то и функция g также является плотностью вероятности
и f(x) = g(x) почти всюду относительно меры Лебега, то и функция g также является плотностью вероятности 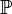 .
.
- Интеграл от плотности по всему пространству равен единице:
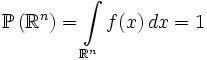 .
.
Обратно, если f(x) — неотрицательная п.в. функция, такая что
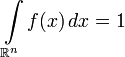 , то существует абсолютно непрерывная вероятностная мера
, то существует абсолютно непрерывная вероятностная мера 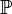 на
на  такая, что f(x) является её плотностью.
такая, что f(x) является её плотностью.- Замена меры в интеграле Лебега:
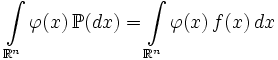 ,
,
где
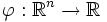 любая борелевская функция, интегрируемая относительно вероятностной меры
любая борелевская функция, интегрируемая относительно вероятностной меры 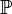 .
.Плотность случайной величины
Пусть определено произвольное вероятностное пространство
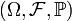 , и
, и 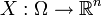 случайная величина (или случайный вектор). X индуцирует вероятностную меру
случайная величина (или случайный вектор). X индуцирует вероятностную меру 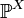 на
на 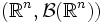 , называемую распределением случайной величины X.
, называемую распределением случайной величины X.Определение 3. Если распределение
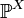 абсолютно непрерывно относительно меры Лебега, то его плотность
абсолютно непрерывно относительно меры Лебега, то его плотность 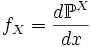 называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.
называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.Таким образом для абсолютно непрерывной случайной величины имеем:
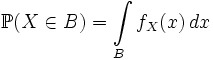 .
.
Замечания
- Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.
- Функция распределения абсолютно непрерывной случайной величины X непрерывна и может быть выражена через плотность следующим образом:
![F_X(x_1,\ldots, x_n) = \mathbb{P}\left(X \in \prod\limits_{i=1}^n (-\infty,x_i]\right) = \int\limits_{-\infty}^{x_n} \!\! \ldots \!\! \int\limits_{-\infty}^{x_1} f_X(x'_1,\ldots, x'_n)\, dx'_1\ldots dx'_n](/pictures/wiki/files/48/06a4ab265241529884a0e84e50be622e.png) .
.
В одномерном случае:
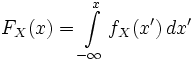 .
.
Если
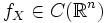 , то
, то 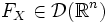 , и
, и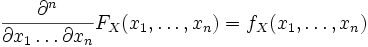 .
.
В одномерном случае:
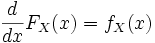 .
.
- Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:
![\mathbb{E}[g(X)] = \int\limits_{\mathbb{R}^n} g(x) \, \mathbb{P}^X(dx) = \int\limits_{\mathbb{R}^n} g(x)\, f_X(x)\, dx](/pictures/wiki/files/56/81e4a19c99cfea91b84be9a3cc5083b3.png) ,
,
где
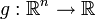 — борелевская функция, так что
— борелевская функция, так что ![\mathbb{E}[g(X)]](/pictures/wiki/files/50/22d55fb83587275b2a82031a3a3ed338.png) определено и конечно.
определено и конечно.Плотность преобразования случайной величины
Пусть
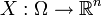 — случайная величина, и
— случайная величина, и 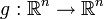 — инъективная непрерывно дифференцируемая функция такая, что
— инъективная непрерывно дифференцируемая функция такая, что 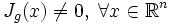 , где Jg(x) — якобиан функции g в точке x. Тогда случайная величина Y = g(X) также абсолютно непрерывна, и её плотность имеет вид:
, где Jg(x) — якобиан функции g в точке x. Тогда случайная величина Y = g(X) также абсолютно непрерывна, и её плотность имеет вид: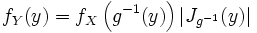 .
.
В одномерном случае:
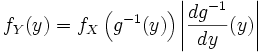 .
.
Примеры абсолютно непрерывных распределений
- Бета распределение;
- Распределение Вейбулла;
- Гамма распределение;
- Распределение Коши;
- Логнормальное распределение;
- Нормальное распределение;
- Непрерывное равномерное распределение
- Распределение Парето;
- Распределение Стьюдента;
- Распределение Фишера;
- Распределение хи-квадрат;
- Экспоненциальное распределение;
- Многомерное нормальное распределение.
См. также
Wikimedia Foundation. 2010.