ЛАПЛАСА УРАВНЕНИЕ

ЛАПЛАСА УРАВНЕНИЕ
ЛАПЛАСА УРАВНЕНИЕ

       
дифференциальное ур-ние с частными производными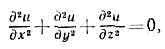
ЛАПЛАСА УРАВНЕНИЕ1
где u(х, у, z) — ф-ция независимых переменных х, у, z. Названо по имени франц. учёного П. Лапласа, применившего его в работах по тяготению (1782). К Л. у. приводят мн. задачи физики и механики, в к-рых физ. величина явл. ф-цией только координат точки. Так, Л. у. описывает потенциал сил тяготения в области, не содержащей тяготеющих масс, потенциал электростатич. поля — в области, не содержащей зарядов, темп-ру при стационарных процессах и т. д. Ф-ции, являющиеся решениями Л. у., наз. гармоническими. Л. у.— частный случай Пуассона уравнения. Оператор наз. оператором Лапласа.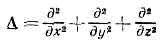
ЛАПЛАСА УРАВНЕНИЕ2

Физический энциклопедический словарь. — М.: Советская энциклопедия. . 1983.

ЛАПЛАСА УРАВНЕНИЕ

- дифференциальное ур-ние 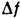2548-52.jpg =0, где 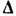2548-53.jpg - Лапласа оператор, а ф-ция f(x1, . . ., х п )отыскивается во всём пространстве Rn или в его части G. Решения Л. у. наз. гармоническими функциями. Каждое решение Л. у. в огранич. области G однозначно выделяется краевыми условиями, накладываемыми на поведение решения (или его производных) на границе 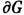2548-54.jpg области G. Если решение отыскивается во всём пространстве Rn, краевые условия сводятся к предписанию нек-рой асимптотики для f при х 1,. . ., 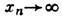2548-55.jpg . Задача о нахождении таких решений наз. краевой задачей. Чаще всего встречаются Дирихле задача, когда на границе задано значение самой ф-ции f, и Неймана задача, когда задано значение производной f по нормали к границе. В случае n=2, когда R можно отождествить с комплексной плоскостью С, всякая гармонич. ф-ция f(x1, х 2) в области 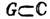2548-56.jpg является вещественной частью нек-рой аналитич. ф-ции 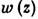2548-57.jpg в этой области (z=x1+ix2). Это обстоятельство позволяет использовать при изучении Л. у. методы теории аналитич. ф-ций. Соответствующее Л. у. неоднородное ур-ние наз. Пуассона уравнением. Л. у. описывает стационарное распределение потенциала (электрич., гравитац. и др. полей) в однородной среде без источников внутри области G. р. А. Минлос.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "ЛАПЛАСА УРАВНЕНИЕ" в других словарях:

  • Лапласа уравнение — Уравнение Лапласа  уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так: и является частным случаем уравнения Гельмгольца. Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном… …   Википедия

  • ЛАПЛАСА УРАВНЕНИЕ — дифференциальное уравнение с частными производными 2 го порядкагде, x, y, z независимые переменные, ?(x, y, z) искомая функция. Рассмотрено П. Лапласом (1782). К уравнению Лапласа приводят многие задачи математической физики (напр., распределение …   Большой Энциклопедический словарь

  • Лапласа уравнение — дифференциальное уравнение с частными производными 2 го порядка . Где х, у, z  независимые переменные, φ(х, у, z)  искомая функция. Рассмотрено П. Лапласом (1782). К Лапласа уравнению приводят многие задачи математической физики (например,… …   Энциклопедический словарь

  • ЛАПЛАСА УРАВНЕНИЕ — однородное дифференциальное уравнение с частными производными вида где функция от пдействительных переменных. Левая часть Л. у. наз. Лапласа оператором от функции и. Регулярные решения Л. у. класса С 2 в нек рой области Dевклидова пространства т …   Математическая энциклопедия

  • Лапласа уравнение —         дифференциальное уравнение с частными производными                   где х, у, z независимые переменные, а u = u(x, y, z) искомая функция. Это уравнение названо по имени П. Лапласа, рассмотревшего его в работах по теории тяготения (1782) …   Большая советская энциклопедия

  • ЛАПЛАСА УРАВНЕНИЕ — численные методы решения методы, заменяющие исходную краевую задачу дискретной задачей, содержащей конечное число N неизвестных, нахождение к рых с соответствующей точностью позволяет определить решение исходной задачи с заданной точностью… …   Математическая энциклопедия

  • ЛАПЛАСА УРАВНЕНИЕ — дифференц. ур ние с частными производными 2 го порядка где х, у, г независимые переменные, и (х, у, г) искомая ф ция. К Л. у. приводит ряд задач физики и техники; ему удовлетворяют, напр., установившаяся темп pa, электрич. потенциал внутри… …   Большой энциклопедический политехнический словарь

  • ЛАПЛАСА УРАВНЕНИЕ — дифференц. ур ние с частными производными 2 го порядка где х, у, z независимые переменные, ф(х, у, z) искомая функция. Рассмотрено П. Лапласом в 1782. К Л. у. приводят мн. задачи матем. физики (напр., распределение темп р в стационарном процессе) …   Естествознание. Энциклопедический словарь

  • Уравнение Лапласа — Уравнение Лапласа  дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так: и является частным случаем уравнения Гельмгольца. Уравнение рассматривают также в двумерном и одномерном… …   Википедия

  • Уравнение в частных производных — Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ)  дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»