ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ

ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ

(функции Бесселя)- решения Z_v(z )ур-ния Бесселя

где параметр (индекс) v -произвольное действительное или комплексное число. В приложениях чаще встречается ур-ние, зависящее от четырёх параметров:

решения к-рого выражаются через Ц. <ф.: u(z) = z^aZ_v(bz^g). Среди ур-ний (2) содержится ур-ние u " -zu = 0, к-рое порождает Эйри функции.

Ц. ф. произвольного порядка. Если v не является целым числом, то общее решение ур-ния (1) имеет вид

где c₁ и c₂- постоянные, J_v и J_-v - ф-ции Бесселя 1-го рода (или Ц. ф. 1-го рода, рис. 1, а). Если v - целое, то J_v и J__v линейно зависимы. Поэтому наряду с J_v(z )вводят ф-ции Бесселя 2-го рода (рис. 1, б) Y_v(z)[иногда их наз. N_v(z)]:

Рис. 1. Графики функций J_v и Y_v вещественного аргу мента x для некоторых целых значений v.

При помощи этих ф-ций общее решение (1) можно всегда записать в виде

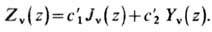
Для приложений важны и др. решения (1) - ф-ции Бесселя 3-го рода, или ф-ции Ханкеля (Ганкеля) 1-го и 2-го рода H_v⁽¹⁾(z )и H_v⁽²⁾(z):

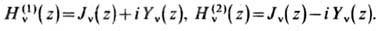
Связь между различным и Ц. ф.:

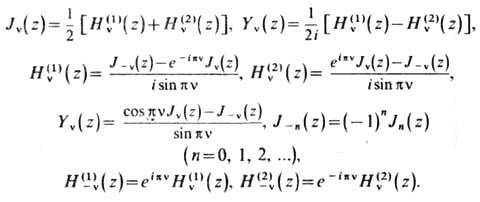
Разложения в ряды:

при n = 0 первую из сумм следует полагать равной нулю, y - логарифмическая производная гамма-функции, y(1) = G'(1) = -g, постоянная Эйлера g = 0,577215.

Интегральные представления Пуассона для ф-ций Бесселя 1-го рода J_v(z )и ф-ций Ханкеля H_v^(1,2)(z) при Rev >:

Интегральные представления Зоммерфельда:

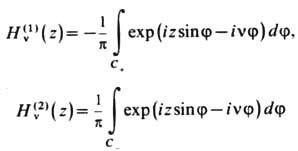
(контуры C₁, C₊, С_ изображены на рис. 2). При v = n (где n- целое)

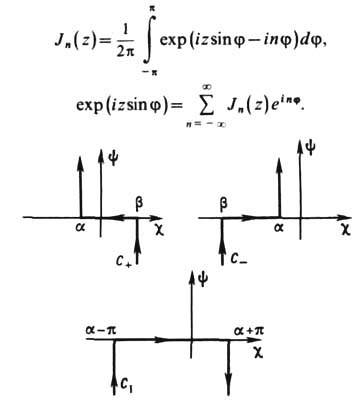
Рис. 2. Контуры интегрирования С_b и C₁ (f = c + iy). Числа a и b связаны соотношением b= abp.

Рекуррентные соотношения и ф-л ы дифференцирования:

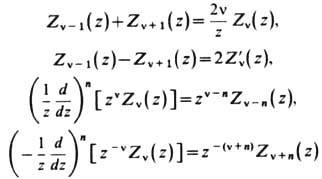
[Z_v(z) - любая из ф-ций J_v(z), Y_v(z), H_v^(1,2)(z)].

Ц. ф. полуцелого порядка. Ц. ф. превращаются в элементарные тогда и только тогда, когда v принимает полуцелые значения (v = n+ 1/2):

Асимптотическое поведение Ц. ф. Для |z|>>1, |z|>> v имеют место оценки:

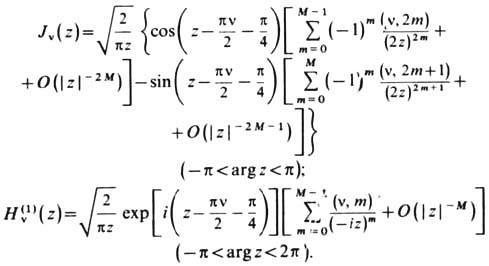
Здесь (v, m) = Г(1/2 + v + m)/[ т!Г(1/2+ v - т)] - т. <н. символ Ханкеля. Выражение для Н _v⁽²⁾(z )аналогично выражению для H_v⁽¹⁾(z), в к-ром (при - 2p<argz<p) i надо заменить на - i.

Интеграл Фурье-Бессeля:

Теорема сложения Графа:

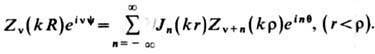
Теорема сложения Гегенбауэра:

Здесь r,r, R - стороны произвольного треугольника; y - угол, лежащий между сторонами R и r; m = сosq; q-угол между сторонами r и r; k - произвольное число; С _n(m) - полином Гегенбауэра (см. Ортогональные полиномы);Z_v(z) -любая из ф-ций J_v(z), Y_v(Z), H_v^(1,2)(z).

Разложение сферич. волны по полиномам Лежандра:

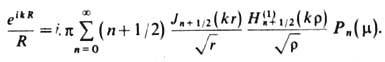
Разложение плоской волны по полиномам Лежандра:

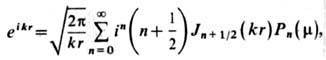
k - волновой вектор; m = соsq; q - угол между векторами k и r.

Модифицированные ф-ции Бесселя (ф-ции Бесселя мнимого аргумента)-решения ур-ния

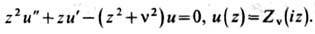
Линейно независимыми решениями при z>0 являются ф-ции

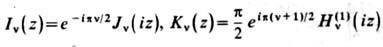
[рис. 3; ф-ции K_v(z) иногда наз. ф-циями Макдональда].

Интегральные представления Пуассона (Re v >-1/2):

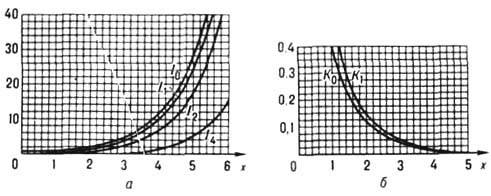
Рис. 3. Графики функций I_v и K_v вещественного аргу мента x для некоторых целых значений v.

Интегральные представления Зоммерфельда для K_v(z)(Re z >0):

Асимптотическое поведение при z+:

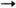Связь между ф-циям и I_v(z) и K_v(z):

Разложение в ряды:

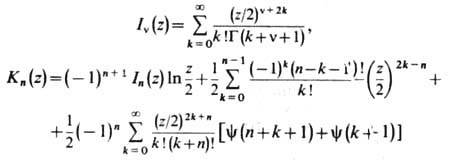
(при n = 0 первую сумму следует полагать равной нулю, y = G').

Рекуррентные соотношения и ф-л ы дифференцирования:

Ф-ц и и I_v(z) и K_v(z) полуцелого порядка:

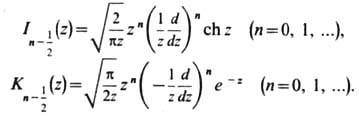
Лит.: Ватсон Г. H., Теория бесселевых функций, пер. с англ., ч. 1,M., 1949; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., M., 1974; Никифоров А. Ф., Уваров В. Б., Специальные функции математической физики, 2 изд., M., 1984; Справочник по специальным функциям..., пер. с англ., M., 1979. А. Ф. Никифоров.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.