- ХАРАКТЕРИСТИЧЕСКИЙ ФУНКЦИОНАЛ
- ХАРАКТЕРИСТИЧЕСКИЙ ФУНКЦИОНАЛ
-
с л у ч а й н о й л и н е й н о й ф у н к ц и и {xj, j
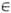Е} - функционал
F(j) на линейном пространстве Е, обобщающий понятие характеристической функции одной случайной величины. Пусть задана линейная случайная функция
т. е. семейство случайных величин (определённых на одном и том же вероятностном пространстве W), помеченных элементами j
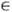Е нек-рого линейного пространства Е и линейно зависящих от них:
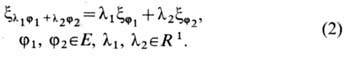
Функционал на Е
наз. X. ф. линейной случайной ф-ции (1). Из (2) и (3) следует, что любого конечного набора элементов j1,..., js ф-ция f{ji}(t1, ..., ts) от вещественных переменных t1,..., ts
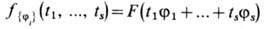
является совместной характеристической ф-цией набора случайных величин {xj1,..., xjs}.. Т. о., X. ф. F(j)однозначно определяет совместные распределения любого конечного набора случайных величин {xj1,..., xjs}, т. е. определяет все статистич. свойства линейной случайной ф-ции (1). X. ф. равен 1 при j = 0, положительно определён, т. е.
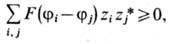
для любого конечного набора элементов j1,..., js и любого набора комплексных чисел z1, ..., zs(* - означает комплексное сопряжение), а также в случае непрерывной линейной ф-ции непрерывен по j. В наиб. простом и употребит. случае - гауссовской линейной случайной ф-ции {xj, j
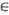Е}. со средним
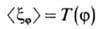
и ковариацией
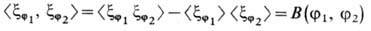
её X. ф.
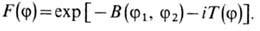
Лит.: Прохоров Ю. В., Сходимость случайных процессов и предельные теоремы теории вероятностей, "Теория вероятностей и ее применения", 1956, т. 1, в. 2, с. 177; Вахания Н. Н., Тари-еладзе В. И., Чобан С. А., Вероятностные распределения в банаховых пространствах, М., 1985. Р. А. Минлос.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
