ФРИДМАНА - РОБЕРТСОНА - УОКЕРА МЕТРИКА

ФРИДМАНА - РОБЕРТСОНА - УОКЕРА МЕТРИКА

- нестационарная метрика четырёхмерного однородного и изотропного пространства-времени с 6-парамет-рической группой симметрии:

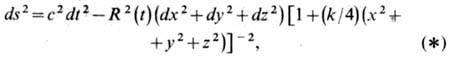
где R(t)- произвольная ф-ция времени t, имеющая размерность длины; х, у, z - безразмерные пространств. координаты; k= - 1, 0, 1.

Ф.- Р.- У. м. как решение ур-ний общей теории относительности была впервые найдена А. А. Фридманом в 1922 для случая k=1 и в 1924 для случая k= -1. Эти результаты были независимо повторены Ж. Леметром (G. Lemaitre) в 1927, после чего важный вклад в её строгий матем. вывод был внесён в 1929, 1933 Г. Робертсоном (Н. P. Robertson), в т. ч. случай k = 0, и в 1936 А. Уокером (A. G. Walker) с помощью методов теории групп для многообразия с максимально симметричными (т. е. однородными и изотропными в любой точке) подпространствами.

Метрика подпространства с координатами х, у, z для каждого / однородна и изотропна в любой точке х, у, z. Для Ф.- Р.- У. м. каждая траектория ( х, у, z) =const есть геодезическая линия, поэтому координаты t, х, у,z образуют сопутствующую систему отсчёта, к-рая в данном случае одновременно является и синхронной (см. Синхронная система). Время t есть собственное время, показываемое покоящимися часами в каждой точке пространства.

Когда для определения ф-ции R (t )и значения k используют ур-ния Эйнштейна с неравным нулю тензором энергии-импульса материи, пространство-время с метрикой (*) наз. космологической моделью Фридмана (иногда, если учитывается космологич. постоянная, её наз. также м о д ел ь ю Л е м е т р а). Для материи с гидродинамич. тензором энергии-импульса

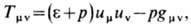
где e - плотность энергии, р- давление, u_m- 4-скорость, условие макс. симметрии подпространства в модели Фридмана выполняется, если r и р - ф-ции только времени, a u_l = u₂ = u₃ =0. При k= -1 (о т к р ы т а я м о д е л ь Ф р и д м а н а) и k = 0 (п л о с к а я м о д е л ь) объём трёхмерного пространства бесконечен, а при k=1(з а к р ы т а я м о д е л ь) он конечен и равен 2p²R³, хотя пространство не имеет границ. Ф-цию R (t )наз. м а с ш т а б н ы м ф а к т ор о м, поскольку дифференциал собств. расстояния между любыми двумя точками модели пропорционален R.

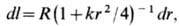
где 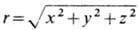. При k=+ 1 после перехода к сферич. координатам и замены c = 2 arctg(r/2) Ф.- Р.- У. м. приводится к виду

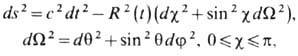
а при k= -1 после замены c = 2 arcth(r/2) - к виду

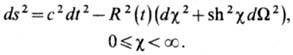
Ф.- Р.- У. м. является основной для совр. космологии, т. к. наблюдаемая часть Вселенной приближённо описывается этой метрикой (с точностью до малых неоднородных возмущений). Из ур-ний для масштабного фактора следует, что в общем случае dR/dt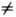0. Отсюда вытекает важнейшее предсказание о нестационарности однородной изотропной Вселенной, к-рое было подтверждено в 1929 открытием Э. Хабблом (Е. P. Hubble) красного смещения галактик, пропорционального их расстоянию от нас.

Важными частными случаями Ф.- Р.- У. м. являются метрика Милна [k= -1, R(t) = t], описывающая Минков-ского пространство-время в нек-рых спец. крординатах (не покрывающих всего многообразия), а также метрика де Ситтера первого рода [k= +1, R (t)= сH₀^-1 ch(H₀t), или k = 0, 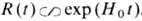, или k= -1,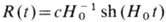

где Н₀ =const] и метрика де Ситтера второго рода [k = -1, R(t) = cH₀^-1 cos(H₀t)], описывающие пространство-время пост. кривизны (см. Де Ситтера пространство-время).

Лит.: Зельдович Я. Б., Новиков И. Д., Строение и эволюция Вселенной, М., 1975; Вайнберг С., Гравитация и космология, пер. с англ., М., 1975; Меллер К., Теория относительности, пер. с англ., М., 1975. И. К. Розгачёва, А. А. Старобинский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.