СТРУКТУРНЫЕ ФАЗОВЫЕ ПЕРЕХОДЫ

СТРУКТУРНЫЕ ФАЗОВЫЕ ПЕРЕХОДЫ

(конфигурационные фазовые переходы, полиморфные превращения) - фазовые переходы в кристаллич. твёрдых телах, состоящие в перестройке структуры этих тел за счёт изменения взаим-ногo расположения отдельных атомов, ионов или их групп и приводящие обычно к изменению типа симметрии кри сталла. С. ф. п. могут происходить при изменении одного или неск. термодинамич. параметров - темп-ры Т, давления p, концентрации компонент (в случае сплава или твёрдого раствора )и др. Наиб. изучены С. ф. п. по темп-ре. Как правило, при понижении Т до Т _к. происходят С. ф. п. из кристаллич. структуры с более высокой симметрией в кристаллич. структуру с более низкой симметрией. При этом исходная и конечная кристаллич. модификации (фазы) могут резко отличаться по свойствам (см. Полиморфизм). С. ф. п. обычно сопровождаются изменением свойств твёрдого тела - упругих, электрических, магнитных и т. п. (см. Сегнетоэлектрики, Сегнетоэла-стики [2, 3 ]).

Если изменяется только точечная симметрия кристалла, то С. ф. п. наз. с о б с т в е н н ы м и, если изменяется трансляционная симметрия,- н е с о б с т в е н н ы м и. Последние приводят к возникновению сверхструктур, как соизмеримых, так и несоизмеримых, а также доменов (ориентацион-ных и трансляционных).

Для определения возможных для данной исходной структуры путей (каналов) перехода в др. структуры используется метод, основанный на теоретико-групповой классификации кристаллич. фаз [1 ].

Многие С. ф. п. сопровождаются изменением фононно-го спектра - появлением в нём т. н. м я г к о й м о д ы, свидетельствующей о неустойчивости данной кристаллич. структуры; одна из оптич. ветвей спектра "смягчается", т. е. щель в ней резко уменьшается, а затухание колебаний резко растёт с приближением Т к Т _к. (см. Колебания кристаллической решётки).

Характерным для С. ф. п. является также появление в фононном спектре т. н. ц е н т р а л ь н о г о п и к а - низкочастотной релаксац. моды малой ширины (по частоте) и высокой интенсивности, связанной с движением доменных стенок вблизи темп-ры перехода Т _к.

Экспериментальные методы. Экспериментально С. ф. п. идентифицируются с помощью дифракц. методов- рентгеновского структурного анализа и нейтронографии структурной (по изменениям межатомных расстояний и объёма элементарной ячейки), по особенностям в поведении теплоёмкости С ( Т )при Т=T _к, а также по изменению скорости звука и упругих модулей решётки. Используются также резонансные методы, основанные на появлении мягкой моды и центр. пика, к-рые детектируются с помощью комбинационного рассеяния света, Мандельштама - Бриллюэна рассеяния, а также неупругого рассеяния нейтронов. Для С. ф. п. с участием магнитоактивных ионов применяются также электронный парамагн. резонанс (ЭПР), ядерный магн. резонанс (ЯМР), мёссбауэровская спектроскопия.

Изменение параметра порядка. Как и любые фазовые переходы, С. ф. п. сопровождаются изменением параметра порядка, к-рый характеризует координац. упорядочение в конденсиров. среде (см. Дальний и ближний порядок). Макроскопич. параметром порядка при описании С. ф. п. может служить изменение локальной плотности кристалла dr(r) = r₂ (r) -r₁ (r)[индексы 1 и 2 соответствуют исходной и конечной фазам; точнее, следует говорить о наборе коэф. разложения dr(r) по неприводимым представлениям исходной группы симметрии кристалла G ]. При микроско-пич. описании параметр порядка строится на векторах смещений атомов относительно их ср. положений (узлов кристаллич. решётки) в исходной фазе.

Среди всех возможных С. ф. п. различают С. ф. п. 2-го рода (типа смещения), при к-рых параметр порядка изменяется плавно и непрерывно, обращаясь в нуль при Т=Т _к, и С. ф. п. 1-го рода (типа порядок - беспорядок), когда параметр порядка испытывает скачок при Т=Т _к. С. ф, п. типа смещения более характерны для простых веществ, тогда как С. ф. п. типа порядок - беспорядок - для бинарных сплавов и твёрдых растворов. Примером С. ф. п. 2-го рода является упорядочение в b-латуни CuZn с ОЦК-структурой или в двухкомпонентных сплавах типа АB(AuCu, CoPt, FePd и др. с ГЦК-структурой). Во всех этих веществах выше Т _к заполнение всех узлов решётки атомами типа А или В происходит равновероятно (вероятности Р _А ⁼ Р _В), чтo соответствует неупорядоченному состоянию. Ниже критич. темп-ры Р _А 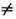Р _B, что соответствует упорядоченному состоянию. При этом возникает сверхструктура, характеризующаяся скалярным параметром порядка | Р _А - Р _B|/(Р _А + Р _B )и волновым вектором k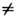0 [4]. Аналогично может быть описано упорядочение в нек-рых фазах внедрения, напр. упорядоченное распределение водорода или дейтерия по междоузлиям Nb и Та в гидридах Nb - H(D) и Та -H(D).

Более сложный (трёхкомпонентный векторный) параметр порядка необходим для описания С. ф. п. типа смещения в сверхпроводящих интерметаллических соединенияхNb₃Sn и V₃Si (пространственная группа симметрии О ³_h), а также в HfV₂ и ZrV₂, находящихся в т. н. ф а з е Л а в е с а (пространственная группа симметрии О ⁷_h). В первом случае кристалл переходит из простой кубич. решётки в тетрагональную (изменение симметрии О ³_h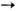D⁹_4h), а во втором - в орторомбическую или ромбоэдрическую (изменение симметрии О ⁷_hD²⁸_2h или D⁵_3d). В обоих случаях элементарная ячейка сохраняется, т. е k =0. В сегнетоэлектриках ВаTiO₃ и SrTiO₃ С. ф. п. происходят посредством смещения ионов относительно октаэдра О ₆ или посредством поворота этого октаэдра.

Образование доменов. Особенностью С. ф. п. по темп-ре является образование доменов в кристалле при Т<Т _к. Поскольку температурное воздействие является скалярным, т. е. не имеет направленности (в отличие, напр., от воздействия механического), то в соответствии с Кюри принципом точечная симметрия кристалла не должна изменяться. Это и приводит к появлению доменной структуры (см. Домены). Симметрия в пределах каждого домена ниже симметрии исходного кристалла, однако расположение доменов определяется элементами симметрии, утраченными при переходе (в простейшем случае образуются т. н. а н т и ф а з н ы е д о м е н ы). При образовании доменов в реальном кристалле существенны энергегич. факторы, граничные условия, дефекты и т. п. [5 ].

Каждый домен должен отличаться от остальных значением тензора деформации, описывающим спонтанную деформацию исходной элементарной ячейки. Внеш. давление снимает вырождение по энергии у доменов и делает энергетически выгодным один из них; при этом фазовая диаграмма кристалла становится более сложной. Напр., в тетрагонально деформированном кристалле при одноосном напряжении изменяется род фазового перехода со 2-го на 1-й и на фазовой диаграмме появляется трикритическая точка. Фазовые диаграммы С. ф. п., содержащие поликритические точки, характерны для многих кристаллов, напр. кристаллов типа перовскитов KMnF₃, CsPbBr₃ и кристаллов типа MnAs, допускающих неск. последовательных С. ф. п., а также магнитные фазовые переходы.

Количественное описание С. ф. п. даётся обычно на основе Ландау теории фазовых переходов с дальнейшими уточнениями (напр., учётом флуктуации параметра порядка). Применяется также приближённое вычисление статис-тич. суммы кристалла, напр. при описании упорядочивающихся сплавов приближением Брэгга - Вильямса (см. Среднего поля приближение), Кирквуда и др. [6] (см. Корреляционная функция).

В основе микроскопич. описания С. ф. п. лежит простой квазиклассич. гамильтониан [6, 7 ], описывающий динамически неустойчивую решётку как набор связанных ангар-монич. осцилляторов [6, 7]:

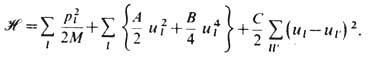
Такой гамильтониан моделирует кристалл с 2 подрешёт-ками, в к-ром атомы одной из них (жёстко фиксированной) создают характерный двухъямный потенциал для подвижных атомов др. подрешётки (см. рис.). Здесь u_l, p_l (в одномерном случае - скалярные величины)-смещение и импульс атома массы М, расположенного в l -м узле кристаллич. решётки; коэф. А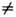0, В и С>0. Коэф. А характеризует модуль упругого сжатия, коэф. В- ангармонизм решётки, С- взаимодействие между атомами в соседних узлах l, l'.

Конфигурационная потенциальная энергия атомов "подвижной" подрешётки в поле атомов "неподвиж ной" подрешётки (одномерный случай).

В системе, описываемой гамильтонианом , при Т _к0 происходит фазовый переход в упорядоченное состояние с конечным ср. смещением 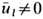. Возможны 2 предельных случая, соответствующие переходам типа смещения и типа порядок - беспорядок. Если при низких темп-pax все подвижные атомы расположены на дне левой потенциальной ямы, то с ростом Т возможна реализация одного из двух случаев: в первом наиб. вероятное положение подвижных атомов соответствует вершине потенциального барьера (переход типа смещения), во втором - дну потенциальной ямы, в результате чего левая и правая ямы заполнены равновероятно (переход порядок - беспорядок). Параметром, различающим эти 2 случая, является отношени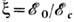е , где 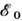=А ²/4 В характеризует глубину ямы (высоту барьера), 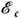= 4 С|А|/В- энергию взаимодействия атомов в разл. ямах на соседних узлах (минимумы двухъямного потенциала соответствуют смещениям ) .

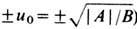При x>>1, А<0. (предельный случай перехода порядок- беспорядок) каждый подвижный атом локализован вблизи дна ямы при всех Т, кроме Т>>Т _к. Т. о., в гармонии, приближении все колебания атомов вблизи высоко-температурного положения равновесия (вершины барьера) неустойчивы; в этом случае осн. динамич. процессы - прыжковые за счёт туннелирования атомов между соседними ямами в одном узле. Такая ситуация может быть описана с помощью эфф. спинового гамильтониана [2, 3], а при высоких темп-pax - моделью, соответствующей невзаимодействующим ангармонич. осцилляторам. При x<< 1, А> 0 (предельный случай перехода типа смещения) неустойчивой оказывается небольшая часть длинноволновых колебаний вблизи высокотемпературного положения равновесия; ниже T _к происходит "замораживание" мягкой фононной моды. В одномерном случае гамильтониан допускает возможность точных решений ур-ний динамики, к-рые обнаруживают 2 типа элементарных возбуждений в системе: фононы с малой амплитудой колебаний и соли-тоны (доменные стенки) - с большой [6] (см. также Точно решаемые модели в с т а т и с т и ч. ф и з и к е).

Одномерный гамильтониан применим, напр., для описания упорядочения протонов в соединениях с водородными связями (КН ₂ РО ₄, биополимеров и др.). Для реальных трёхмерных кристаллов следует учитывать анизотропию энергии межатомного взаимодействия U_c, обладающую не двумя, а большим числом локальных минимумов разл. глубины. Существен также учёт взаимодействия решётки с электронной подсистемой (особенно в металлах) и спиновой (в магнетиках) [6]. Напр., в фононном спектре нек-рых переходных металлов и сплавов возможно "смягчение" фононов с волновым вектором 2k_F, где (2p/h)k_F - импульс Ферми (коновская особенность). С др. стороны, электрон-фононное взаимодействие может приводить к т. н. п а й-е р л с о в с к о й н е у с т о й ч и в о с т и (см. Пайерлса переход )и связанному с ней С. ф. п.- спонтанному искажению решётки с волновым вектором 2k_F. При этом в электронном спектре возникает щель (см. Переход металл - диэлектрик), а распределение заряда описывается волной зарядовой плотности. Аналогично сильное спин-решёточное взаимодействие в нек-рых сплавах переходных и редкоземельных металлов (гигантская магнитострикция )также приводит к С. ф. п.

Лит.:1) Изюмов Ю. А., Сыромятников В. Н., Фазовые переходы и симметрия кристаллов, М., 1984; 2) Блинц Р., Жекш Б., Сегнетоэлектрики и антисегнетоэлектрики, пер. с англ., М., 1975; 3) Вакс В. Г., Введение в микроскопическую теорию сегнето-электриков, М., 1973; 4) Матвеева Н. М., Козлов Э. В., Упорядоченные фазы в металлических системах, М., 1989; 5) Жири-фалько Л., Статистическая физика твердого тела, пер. с англ., М., 1975; 6) Брус А., Каули Р., Структурные фазовые переходы, пер. с англ., М., 1984; 7) Бётгер X., Принципы динамической теории решетки, пер. с англ., М., 1986; 8) Толедано Ж.-К., Толеда-но П., Теория Ландау фазовых переходов, пер. с англ., М., 1994.

Ю. Г. Рудой.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.