СОБСТВЕННЫЙ ВЕКТОР

СОБСТВЕННЫЙ ВЕКТОР

оператора- ненулевой вектор из векторногопространства L, к-рый переводится данным оператором в пропорциональныйему вектор, т. е.

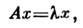
где вещественное либо комплексное число 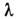наз. собственным значением оператора А. С. в. операторов, <действующих в функциональном пространстве, наз. собственными функциями.

Для линейного оператора А множество 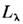всех С. в., отвечающих одному и тому же собств. значению 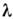,образует линейное подпространство, к-рое наз. собств. подпространством А. Если пространство L конечномерно (n -мерно), а матрицапреобразования А эрмитова, то у неё имеется ровно п различныхС. в., отвечающих вещественным собств. значениям.

Наличие С. в. у операторов в бесконечномерных пространствах - явлениедовольно редкое, хотя для физ. приложений существенно, что операторы спец. <классов (интегральные, дифференциальные и т. п.) часто обладают обширныминаборами С. в. Наиб. важным для физики бесконечномерным векторным пространствомявляется пространство l² векторов f, g вида (a₁,a₂,...), (b₁, b₂,...) со скалярнымпроизведением 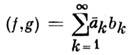(черта означает комплексное сопряжение) и соответствующей конечной нормой 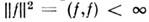.Это пространство изоморфно пространству квадратично интегрируемых ф-ций 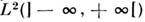и обладает всеми свойствами последнего.

В конечномерных пространствах, наоборот, у всякой n-мерной матрицы . имеетсяхотя бы один С. в., отвечающий, вообще говоря, комплексному собств. значению 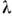,а если к тому же матрица А невырождена,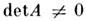, то у такой матрицы найдутся ровно п разл. комплексных С. в. Этосправедливо, в частности, для унитарных конечномерных матриц 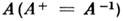В физ. приложениях часто возникает необходимость разложить произвольныйвектор в сумму по С. в. заданной эрмитовой матрицы А[напр., привестик диагональному виду симметричную квадратичную форму ( хАх)]. Этазадача решается переходом с помощью унитарного преобразования к базису, составленномуиз С. в. матрицы А. В этом базисе действие оператора А сводитсяк умножению каждого базисного вектора на соответствующее ему собств. значение 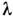.В бесконечномерном случае аналогом этой процедуры диагонализации являетсят. н. спектральное разложение.

Лит. см. при ст. Собственные функции. Л. О. Чехов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.