- ЗАРЯЖЕННЫЙ ТОК
- ЗАРЯЖЕННЫЙ ТОК
-
ток в квант. теории поля, изменяющий на единицу электрич. заряды ч-ц (в отличие от нейтрального тока, не меняющего заряды). З. т. входит в лагранжиан слабого взаимодействия и состоит из лептонной и адронной частей. Напр., b-распад нейтрона n® p+e-+v^e описывается вз-ствием лептонного и адронного З. т. В этом процессе изменяются заряды как в лептонной (e-v^e), так и в адронной (пр) вершинах Фейнмана диаграммы (рис.).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЗАРЯЖЕННЫЙ ТОК
-
(заряженный слабый ток) - один из фундаментальных операторов теории слабого взаимодействия, обусловливающий переходы, при к-рых электрич. заряд конечных и нач. частиц (лептонов, адронов) меняется на единицу (в единицах элементарного электрич. заряда е).3. т. jm( х) (x- пространственно-временная точка, m=0,1, 2, 3) представляетсобой сумму лептонного j lm ( х )и адронного (кваркового) j qm ( х) токов: jm ( х)= j lm ( х)+ j qm(x), каждый из к-рых является суммой векторного и аксиального токов.
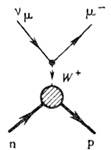
Примером процесса, обусловленного как лептонным, так и адронным 3. т., является квазиупругое рассеяние нейтрино на нейтроне: nm+n " m-+p (рис.). Как видно из рисунка, заряд меняется на -1 в лептонной (nmm-) и на +1 в адронной (рn) вершинах циаграммы Фейнмана. <В плотность лагранжиана слабого взаимодействия 3. т. входит след. образом:
 эрмитово сопряжённое слагаемое. Здесь Wm( х) -- поле заряж. промежуточных векторных бозоновWb, g- безразмерная константа взаимодействия (в единицах
эрмитово сопряжённое слагаемое. Здесь Wm( х) -- поле заряж. промежуточных векторных бозоновWb, g- безразмерная константа взаимодействия (в единицах  =с=1). В области квадратов передач 4-импульса, много меньших т2W (mW- масса W-бозона), плотность эффективного гамильтониана слабого взаимодействия имеет вид:
=с=1). В области квадратов передач 4-импульса, много меньших т2W (mW- масса W-бозона), плотность эффективного гамильтониана слабого взаимодействия имеет вид:
( j +m - ток, эрмитово сопряжённый jm ), - фермиевская константа слабого взаимодействия. <В соответствии с данными опытов в лептонный ток входят только левые L компоненты полей лептонов (см. Киральность):
- фермиевская константа слабого взаимодействия. <В соответствии с данными опытов в лептонный ток входят только левые L компоненты полей лептонов (см. Киральность):
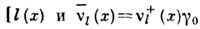 - операторы полей заряж. лептонов (е, m, t) и соответствующих нейтрино (ne, nm, nt),gm,g5 - Дирака матрицы]. Ток j lm (x) построен так, что сохраняются по отдельности электронное, мюонное и таонное лептонные числа. Адронный 3. т. Кабиббо [Н. Кабиббо (N. Cabibbo), 1963] имеет вид:
- операторы полей заряж. лептонов (е, m, t) и соответствующих нейтрино (ne, nm, nt),gm,g5 - Дирака матрицы]. Ток j lm (x) построен так, что сохраняются по отдельности электронное, мюонное и таонное лептонные числа. Адронный 3. т. Кабиббо [Н. Кабиббо (N. Cabibbo), 1963] имеет вид:
где qC- Кабиббо угол, первое слагаемое - 3. т., не изменяющий странности S, второе слагаемое - ток, изменяющий S на единицу. Векторная часть тока jCm (DS = 0) сохраняется (см. Векторного тока сохранение). Аксиальная часть тока jm (DS = 1) удовлетворяет условию частичного сохранения аксиального тока (см. Аксиального тока частичное сохранение);его матричные элементы отличны от нуля только в случае, если удовлетворяются правила отбора DQ=DS и DI = 1/2 (Q- электрич. заряд, I - изотопич. спин). Через операторы полей и-, d- и s-кварков ток Кабиббо записывается след, образом: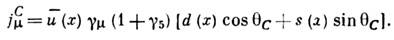
Если бы полный адронный 3. т. совпадал с током Кабиббо, то в калибровочных теориях электрослабого взаимодействия возник бы изменяющий странность нейтральный ток, к-рый на опыте не наблюдается (напр., относит. вероятность распада меньше6.10-7). Чтобы избежать этого, к току Кабиббо необходимо добавить 3. т. Глэшоу - Илиопулоса - Майани (ГИМ) [Ш. Глэшоу (Sh. Glashow), Дж. Илиопулос (J. Iliopulos), Л. Майани (L. Maianij, 1970], в к-рый входит дополнительный, очарованный, кварк с:
меньше6.10-7). Чтобы избежать этого, к току Кабиббо необходимо добавить 3. т. Глэшоу - Илиопулоса - Майани (ГИМ) [Ш. Глэшоу (Sh. Glashow), Дж. Илиопулос (J. Iliopulos), Л. Майани (L. Maianij, 1970], в к-рый входит дополнительный, очарованный, кварк с:
где с(х) - оператор поля с-кварка. Т. к. sin2qC~0,05, то из (2) следует, что в распадах очарованных частиц должны доминировать каналы, в к-рых образуются странные частицы. Это предсказание теории хорошо подтверждается на опыте. Напр., вероятности распадов D- -мезона по каналам К -+всё и всё составляютсоответственно 16(4)% и 48(15)%, тогда как вероятность распада D+ "p+p+p- равна 0,5(0,2)%. Сумма токов Кабиббо и ГИМ может быть записана в виде:
всё составляютсоответственно 16(4)% и 48(15)%, тогда как вероятность распада D+ "p+p+p- равна 0,5(0,2)%. Сумма токов Кабиббо и ГИМ может быть записана в виде:
ортогональная матрица. Т. <о., в ток входит толькоодин параметр - qC. Если учесть также тяжёлые b- и t-кварки, т. е. добавить в теорию ещё один кварковый дублет, то 3. т. имеет в этом случае существенно более сложную структуру:
входит толькоодин параметр - qC. Если учесть также тяжёлые b- и t-кварки, т. е. добавить в теорию ещё один кварковый дублет, то 3. т. имеет в этом случае существенно более сложную структуру:
Здесь U - унитарная 3 X 3 матрица, введённая в 1973 М. Кобаяси (М. Kobayashi) и К. Маскава (К. Maskawa). Она характеризуется тремя углами и одной фазой. Если фаза отлична от нуля, то это означает, что слабое взаимодействие не инвариантно относительно СР-преобразования. Все известные слабые процессы, обусловленные 3. т., могут быть описаны с помощью выражений (1) и (3). Лит.: Биленький С. М., Лекции по физике нейтринных и лептон-нуклонных процессов, М., 1981; Окунь Л. Б., Лептоны и кварки, М., 1981. С. М. Биленький.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
