ЗАРЯДОВОЕ СОПРЯЖЕНИЕ

ЗАРЯДОВОЕ СОПРЯЖЕНИЕ

       

(С), операция замены всех ч-ц, участвующих в к.-л. вз-ствии, на соответствующие им античастицы. Опыт показывает, что сильное и эл.-магн. вз-ствия не меняются при З. с., то есть сильные и эл.-магн. вз-ствия ч-ц и античастиц, находящихся в тех же состояниях, одинаковы. Это означает, что для любого процесса, происходящего с к.-л. ч-цами под действием сильного или ал.-магн. вз-ствия, существует в точности такой же процесс для их античастиц.

Симметрия законов сильного и эл.-магн. вз-ствий относительно замены ч-ц на античастицы приводит к тому, что для истинно нейтральных частиц (или систем) сохраняется особая величина — зарядовая чётность. В слабом взаимодействии, обусловливающем, в частности, большинство распадов ч-ц, отсутствует симметрия относительно З. с. Поэтому, напр., геом. хар-ки распада ч-ц отличны от хар-к распада соответствующих античастиц: если продукты распада ч-цы вылетают преим. в одну сторону, то продукты распада античастицы — в противоположную сторону. В процессах слабого вз-ствия отсутствует также зеркальная симметрия — симметрия между «правым» и «левым» направлениями в пр-ве (см. ПРОСТРАНСТВЕННАЯ ИНВЕРСИЯ). (см. КОМБИНИРОВАННАЯ ИНВЕРСИЯ).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ЗАРЯДОВОЕ СОПРЯЖЕНИЕ

(С-преобразование) - операция замены частиц соответствующими античастицами. Оператор 3. с.определяется след. образом. Если обозначить вектор состояния системы частиц а через |а>, а вектор состояния системы соответствующих античастиц с теми же импульсами и проекциями спинов через то

где С (а) - фазовый множитель, | С(а) |=1. Т. к. истинно нейтральная частица (система частиц) тождественна своей античастице, то в этом случае и

Множитель С(а) в (2) может принимать значения b1 и наз. зарядовой чётностью частицы (системы частиц) или С-чётностъю. Если гамильтониан взаимодействия коммутирует с оператором то взаимодействие инвариантно относительно 3. с. При этом матричные элементы С-сопряжённых процессов - античастицы, у к-рых импульсы и проекции спинов такие же, как у частиц а, b, с, d) связаны соотношением: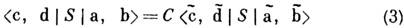

(где S - матрица рассеяния, С - фазовый множитель), из к-рого могут быть получены соотношения между измеряемыми на опыте величинами. Напр., из (3) следует, что для процесса перпендикулярные к плоскости реакции компоненты векторов поляризации L- и -гиперонов должны быть одинаковыми. <Если нач. система обладает определ. С-чётпостью, то из инвариантности относительно 3. с. вытекает, что конечная система должна обладать той же С-чётностью. Из эксперим. данных по проверке принципов инвариантности следует, что сильное и эл.-магн. взаимодействия инвариантны относительно 3. с. Поэтому, напр., p⁰ -мезон распадается (за счёт эл.-магн. взаимодействия) на два g-кванта, а распад p⁰ " 3g запрещён. На опыте последний распад действительно не наблюдается (верх. граница отношения вероятностей распадов p⁰ " Зg к p⁰ "2g R<1,5.10^-6). Из С-инвариантностивытекает также, что спектры p⁺- и p^- -мезонов в распаде h " p⁺+p^-+p⁰ (вызываемом сильным взаимодействием) должны быть одинаковыми. Данные опыта показывают, что зарядовая асимметрия
А = (N⁺-N^-)/(N⁺ +N^-)= 0,28 (26).10^-2
(где N^+/-- число событий с энергией p^b -мезонов большей, чем энергия p^-/+ в системе покоя h-мезона). Это значение согласуется с А=0.Слабое взаимодействие нарушает инвариантность относительно 3. с. Это следует уже из первого опыта Ц. С. By (С. S. Wu) с сотрудниками, доказавшего несохранение пространств. чётности в слабом взаимодействии (см. Чётность). В этом эксперименте была обнаружена асимметрия в угловом распределении электронов, образующихся при (b-распаде поляризованного ⁶⁰ Со. Такая асимметрия может возникать, если в угловое распределение входит член <s> р, где <s> - вектор поляризации ядер ⁶⁰ Со, р - импульс электронов; оно инвариантно относительно обращения времени Т (при изменении знака времени <s> и р меняют знак), но меняет знак при пространств. инверсии Р ( р преобразуется как вектор, a <s> как псевдовектор), поэтому в силу теоремы СРТ С-инвариантность также оказывается нарушенной. Лит.: Мэтьюс П., Релятивистская квантовая теория взаимодействий элементарных частиц, пер. с англ., М., 1959; Новожилов Ю. В., Введение в теорию элементарных частиц, М., 1972; Бьёркек Д. Д., Д р е л л С. Д., Релятивистская квантовая теория, пер. с англ., т. 2, М., 1978; Окунь Л. Б., Лептоны и кварки, М., 1981. С. М. Биленький.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.