РЕДУКЦИОННЫЕ ФОРМУЛЫ

РЕДУКЦИОННЫЕ ФОРМУЛЫ

- правила вычисления элементов матрицы рассеяния (S) в аксиоматической квантовой теории поля (АКТП). Конкретный вид Р. ф. зависит от выбора исходных объектов в конкретном варианте теории. Наиб. прост этот вид для АКТП в формулировке Боголюбова, где исходным объектом является сама 5-матрица, понимаемая как оператор в Фока представлении:

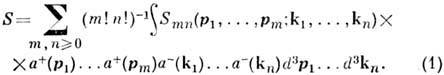
Здесь 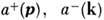- операторы рождения и уничтожения частиц с импульсами соответственно p и k. Для S в нормальной форме (1) вычисление матричного элемента перехода 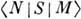между свободными m -части-чным нач. состоянием 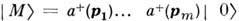и n - частичным конечным состоянием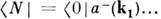

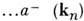сводится к использованию канонических перестановочных соотношений и даёт коэффициентную ф-цию S_mn плюс члены, пропорц. дельта-функции (они отвечают несвязным Фейнма-на диаграммам).

В релятивистской теории нормальную форму (1) удобно переписать в релятивистски-инвариантном виде, через нормальное произведение свободных полей f(x):

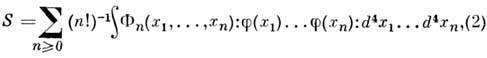
где коэф. разложения Ф _n зависят от пространственно-временных координат x_i. Тогда Р. ф. даются перестановочными соотношениями оператора О, заданного нормальным разложением типа (2), с операторами

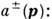
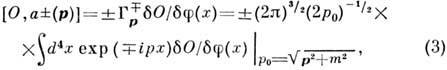
интегральные операции 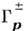осуществляют преобразование Фурье и переводят 4-импульсы р( р₀, р )на массовую поверхность: р² = m² (m - масса частицы; используется система единиц, в к-рой с -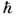=1). Последоват. выполнение коммутаций 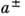сначала с S, а затем с её вариац. производными приводит элемент S к неск. эквивалентным формам. Разные формы удобны для выявления следствий разд. аксиом теории; все они используются при исследовании аналитич. свойств амплитуд рассеяния и многочастичных процессов, напр. при доказательстве дисперсионных соотношений в АКТП. В частности, Р. ф.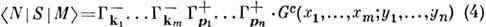

(плюс несвязные вклады) связывает матричный элемент с причинной Грина функцией G^c, через к-рую с помощью преобразования Фурье выражается амплитуда перехода вне массовой поверхности:

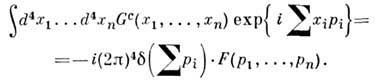
В формулировке Лемана - Симанзика - Циммермана (Н. Lehmann, К. Symanzik, W. Zimmermann, 1955) исходным объектом теории служит взаимодействующее (интерполирующее) поле А(х). Асимптотич. состояния при 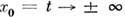строятся как пределы

состояний, полученных действием на вакуум 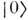сглаженных операторов: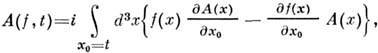

где f(x)- гладкие решения Клейна- Гордона уравнения (волновые пакеты),

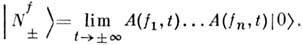
Теорема Хаага - Рюэля (R. Haag, D. Ruelle, 1962) утверждает, что в АКТП эти пределы существуют вследствие аксиом Уайтмана. При этом 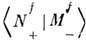= 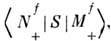а при снятии сглаживания, когда f_i(x)

становится плоской волной с импульсом р_i и энергией 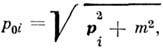состояние 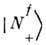переходит в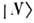

Р. ф. Лемана - Симанзика - Циммермана связывает фигурирующую в (4) причинную ф-цию Грина с хронологическим произведением взаимодействующих полей:

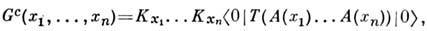
где .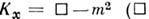- Д'Аламбера оператор).

Лит.: Швебер С., Введение в релятивистскую квантовую теорию поля, пер. с англ., М., 1963; Ициксон К., 3ю-6ер Ж.- Б., Квантовая теория поля, пер. с англ., т. 1, М., 1984; Боголюбов Н. Н., Логунов А. А., Ок-сак А. И., Тодоров И. Т., Общие принципы квантовой теории поля, М., 1987. В. П Павлов

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.