ПУАНКАРЕ ТЕОРЕМА

ПУАНКАРЕ ТЕОРЕМА

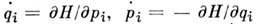
о возвращении - одна из осн. теорем, характеризующих поведение динамической системы с инвариантной мерой. Примером такой системы является гамилътонова система, эволюция к-рой описывается решениями Гамильтона уравнений 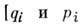- канонич. координаты и импульсы; i = 1, ..., n; H = Н (р, q)- Гамильтона функция; точкой обозначено дифференцирование по времени t]. Инвариантной (сохраняющейся

при эволюции) мерой служит объём

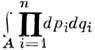
области А в фазовом пространстве М, сохраняющийся в соответствии с Лиувилля теоремой. Согласно П. т., через любую окрестность U любой точки x = ( р _i, q_i), принадлежащей инвариантному множеству конечной положительной меры из М, проходит траектория, к-рая возвращается в U. П. т. доказана А. Пуанкаре в 1890.

Общая динамич. система описывается однопарамет-рич. группой отображений 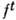фазового пространства на себя: для точки x из М 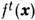= x(t), причём 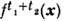= 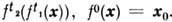В общем случае М- нек-рое пространство с мерой m, инвариантность к-рой означает, что= m(А )для любой области А из М.

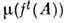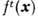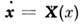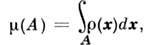Напр.,если - решение системы дифференц. ур-ний с нач. условием то инвариантная мера где 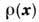- неотрицат. решение Лиувилля уравнения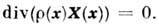

Если ф-ция Гамильтона Н не зависит от времени явно, она сохраняется, а траектории не покидают поверхность уровня М _с: Н(р, q)= с в М. При grad Н. 0 на М _с инвариантная мера на поверхности уровня задаётся соотношением dm= ds/|gradH|, где ds- элемент объёма на М _с .

В общем случае П. т. утверждает, что у динамич. системы с конечной инвариантной мерой для почти всех точек 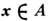при m( А)> 0 траектория 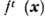возвращается в А: найдётся такое 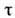> 1, что 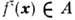. При нек-рых предположениях относительно М11. т. усиливается: траектории возвращаются в А бесконечное число раз, т. е. устойчивы по Пуассону.

Примеры: в гамильтоновой системе ур-ний c = у, 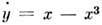все траектории, кроме траекторий, лежащих на уровне 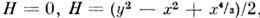, являются периодическими, поэтому возвращаются в любую свою окрестность. Отображение f тора Т² с координатами 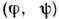(mod 2p), задаваемое соотношением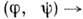

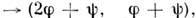сохраняет площадь. Здесь периодических точек счётное множество, а через множество полной меры проходят траектории, не являющиеся периодическими, но устойчивые по Пуассону.

Пусть F- любая непрерывная ф-ция на фазовом пространстве М динамич. системы 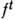, удовлетворяющей условиям П. т. Тогда для почти всякой точки 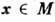и любого, сколь угодно малого e > 0 найдётся последовательность значений 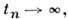для к-рой 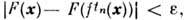т. е. значение F(x )при движении вдоль траектории повторяется с любой заданной точностью. На это утверждение опирается известный парадокс классич. статистич. механики (парадокс возвратов Пуанкаре - Цермело), однако, строго говоря, ни одна из используемых для построения этого парадокса ф-ций (энтропия и т. д.) не является ф-цией на фазовом пространстве.

Лит.: Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.- Л., 1949; Арнольд В. И., Математические методы классической механики, 2 изд., М., 1979. Л. М. Лерман.

Явление выхода и возвращения точек области А в заданное с определ. точностью микроскопич. состояние - слишком нерегулярный процесс, чтобы его можно было оценить одним характерным временем, называемым временем возвращения Пуанкаре. Ср. время возвращения (цикл Пуанкар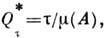е) где 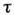- промежуток между измерениями; инвариантная мера 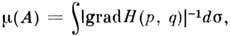где интегрирование проводится по изоэнергетич. поверхности Н(р, q) -= const.

П. т. не даёт конструктивного построения самого возвращения и нуждается в его реализации с помощью нек-рого случайного процесса. Ср. время возвращения удалось оценить М. Смолуховскому (М. Smoluchowski, 1915) с помощью случайного процесса, моделирующего броуновское движение. Он показал, что цикл Пуанкаре значительно больше вероятного времени возвращения наблюдаемого макроскопич. состояния в исходное равновесное состояние.

П. т. рассматривает динамич. системы со строго фиксиров. энергией 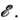В статистич. физике им соответствуют системы, описываемые микроканонич. распределением Гиббса (см. Гиббса распределения). Энергия этих систем задана с точностью 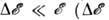можно принять равной ср. флуктуации энергии). Число состояний, находящихся в слое 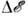[определяемое статистич. весом W (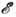, V, N), где N- число частиц, V- объём], чрезвычайно велико. Аналогичное рассмотрение возможно и для др. ансамблей Гиббса.

Реальное время возвращения системы из неравновесного состояния к статистич. равновесию может быть оценено на основании Онсаеера гипотезы, предполагающей, что затухание больших флуктуации происходит по законам термодинамики неравновесных процессов. Хотя большие флуктуации очень редки, все следствия гипотезы Онсагера хорошо подтверждаются экспериментально и позволяют установить связь между кинетическими коэффициентами и равновесными флуктуациями потоков (см. Грина- Кубо формулы).

Лит.: Смолуховский М., Молекулярно-теоретиче-ские исследования по вопросу об обращении термодинамически необратимых процессов и о возврате аномальных состояний, в сб.: Эйнштейн А., Смолуховский М., Броуновское движение, пер. с нем., М., 1936, с. 273; Кац М., Вероятность и смешные вопросы в физике, пер. с англ., М., 1965.

Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.