ПРАВИЛА СУММ

ПРАВИЛА СУММ

- теоретич. соотношения, фиксирующие значение нек-рой суммы (интеграла) матричных элементов, характеризующих переходы между состояниями рассматриваемой системы. Широкое применение П. с. в физике связано с тем, что во мн. случаях из теоретич. соображений удаётся вычислить лишь нек-рую сумму физ. матричных элементов, но каждый отд. член суммы теоретически не вычисляется. Однако он может быть измерен экспериментально. Т. о. возникает возможность проверки теоретич. принципов, лежащих в основе конкретного класса П. с.

Правила сумм в квантовой механике и квантовой теории поля. По-видимому, существование П. с. обусловлено вероятностным характером предсказаний квантовой механики. Простейшим и наиб. фундаментальным П. с. является утверждение о том, что полная вероятность найти систему в одном из возможных состояний равняется единице. В более общем виде это утверждение представляется в форме условия полноты базисного набора векторов состояний:

где I - единичный оператор,- вектор состояния, описывающий систему в состоянии с полным набором собств. значений причём может пробегать как дискретный, так и непрерывный ряд значений; - комплексно сопряжённый вектор ("кет" и "бра" векторы Дирака).

Вывод П. с. подразумевает переход от операторного соотношения (1) к матричным элементам. Стандартным приёмом служит рассмотрение нек-рого перестановочного соотношения, напр.:

где (k,l =1,2,3) - операторы компонент координаты и импульса,- гамильтониан, т- масса (здесь и далее постоянная Планка принята равной единице). Обращаясь к матричному элементу (1а) по нек-рому состоянию j и пользуясь (1), получаем П. с.

где здесь- энергии состояний (М. Борн, М. Вот,В. Гейзенберг, W. Heisenberg, П. Йордан, P. Jordan, 1926).

Наиб. известным частным случаем соотношений (2) является П. с. Томаса - Райхе - Кюна (W. Thomas, F. Reiche, W. KUhn, 1925) для вероятностей дипольных (излучательных) радиац. квантовых переходов в атомах:

где вектор описывает атом в осн. состоянии 15, описывает атом в Р -состоянии с гл. квантовым числом п;- классич. радиус электрона, - частота перехода Если выразить вероятности переходов через соответствующие силы осцилляторов, получим др. форму записи П. с. Томаса - Райхе - Кюна (см. Сила осциллятора). Подобный метод вывода П. с. получил широкое распространение в физике адронов. Исходными при этом являются перестановочные соотношения между операторами разл. векторных (см. Векторный ток )и аксиальных токов адронов, или алгебра токов. Необходимость обращения к вспомогат. объектам - токам связана с тем, что наблюдаемые адроны не являются фундам. объектами и с точки зрения квантовой теории поля описываются сложной (и неизвестной) волновой ф-цией элементарных составляющих - кварков и глюонов. Что касается токов, то они, с одной стороны, являются простыми билинейными комбинациями фундам. полей кварков, с др. стороны - их матричные элементы могут быть измерены в слабых и эл.-магн. переходах между адронами. В частности, рассмотрение перестановочных отношений между компонентами электромагнитного тока адронов приводит к П. с. Дрелла - Хёрна - Герасимова (S. Drell, А. Неагп, С. Б. Герасимов, 1966):

где - полное сечение взаимодействия фотона (с энергией v) с поляризов. протоном, причём спин фотона параллелен ( Р )или антипараллелен ( А )спину протона, 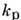- аномальный магнитный момент протона - масса протона.

Возможности эксперим. проверки П. с., следующих из алгебры токов, значительно облегчаются применением гипотезы аксиального тока частичного сохранения:

где - аксиальный ток кварков в состоянии с изотопич. спином I = 1, - константа распада - масса мезона, - поле мезона.

Предполагается также, что 4-импульс, переносимый током, близок к нулю. Соотношение (3) позволяет во мн. случаях перейти от матричных элементов аксиального тока, к-рые экспериментально известны лишь в небольшом числе случаев, к амплитудам с участием мезонов.

Наиб. известным следствием алгебры операторов аксиальных токов и гипотезы частичного сохранения аксиального тока является правило сумм Адлера - Вайсбергера (S. Adler, W. Weisberger, 1965):

где k,u - импульс и энергия мезона в лаб. системе, - полное сечение взаимодействия с протоном, -аксиальная константа бета-распада нейтрона - константа связи мезона с нуклоном .

Особенно наглядный характер имеют П. с. в модели партонов Р. Фейнмана (R. Feynman, 1970). Так, для заряда протона можно написать

где - ф-ции распределения u-, d-,s-кварков (антикварков) в протоне, x- доля импульса протона, приходящаяся на партон; нормировка такова, что каждый член в левой части (5) имеет смысл числа соответствующих кварков (антикварков). Ф-ции распределения кварков могут быть выражены через сечения глубоко неупругих процессов и доступны непо-средств. эксперим. определению. П. с. (5) позволяют убедиться, что целочисленный заряд адронов составлен из дробных зарядов кварков. В 1988 с помощью подобных соотношений измерена доля спина протона, приходящаяся на кварки. Оказалось, что, вопреки наивным ожиданиям, она близка к нулю. Этот результат получил назв. "спинового кризиса" и указывает на необходимость учёта вклада глюонов в спин нуклона. Более конкретной формулировкой "спинового кризиса" является близость к нулю матричного элемента от изотопически синглетного аксиального тока по протону:

где - Дирака матрицы, p- волновая ф-ция протона; и, d, s- волновые ф-ции кварков.

П. с. для адронов имеют, строго говоря, интегральный характер, поскольку спектр в рассеянии частиц непрерывен. Однако реально в П. с. доминируют, как правило, резонанса, с наименьшей массой. Так, в П. с. Адлера - Вайсбергера (4) в интеграле от разности се-ченпй наиб. велик вклад изобары (1240). Поэтому было предложено много П. с., в к-рых интегралы заменяются на суммы вкладов резонансов, причём в суммах оставляют 1-2 первых члена. По-видимому, наиб. известным примером такого рода является П. с. Вайн-берга (S. Weinberg, 1967) для сечений аннигиляции - в адроны. Из этих П. с. следует, в частности, соотношение между массами и -мезонов:

к-рое хорошо согласуется с результатами экспериментов.

Обнаруженная эмпирически возможность аппроксимации кривых для сечений вкладов отд. резонансов получила наиб. общее выражение в принципе дуальности. Согласно этому принципу, сечения могут вычисляться либо как гладкие кривые в простых, прежде всего партонных, моделях, либо как вклад резонансов. Результаты должны совпадать после усреднения вкладов резонансов по нек-рому характерному интервалу энергий (порядка 1 ГэВ). В частности, Дж. Сакураи (J. Sakurai, 1973) предложил след. форму сечения аннигиляции в адроны:

где s - квадрат полной энергии в системе центра инерции, сумма берётся по векторным мезонам, - масса мезона,- ширина его распада на Предполагается далее, что при сумма по векторным мезонам стремится к константе. Значение константы должно быть нормировано на вклад низшего состояния ( -мезона). П. с., следующие из принципа дуальности, хорошо согласуются с экспериментом.

Принцип дуальности получил теоретич. обоснование и точную формулировку в рамках квантовой хромоди-намики (КХД). Эфф. константа взаимодействия КХД мала только на малых расстояниях. Связывание же кварков и глюонов в адроны происходит на расстояниях, где взаимодействие становится сильным, в результате чего ещё не удалось найти аналитич. методы вычисления характеристик адронов. Поэтому метод П. с. в приложениях к КХД и физике адронов имеет принципиальный характер. В качестве примера применения П. с. в КХД рассмотрим амплитуду перехода фотона в адроны и обратно. Эта амплитуда является аналитич. ф-цией единственной переменной - квадрата 4-им-

пульса фотона . Если (- масса кварка), то возможен реальный распад фотона в адроны. Это означает, что амплитуда имеет мнимую часть. Мнимую часть не удаётся вычислить в КХД, но её можно определить экспериментально, измеряя сечение аннигиляции (через виртуальный фотон) в адроны. Дисперсионных соотношений метод позволяет определить интересующую нас аналитич. ф-цию при любых через её мнимую часть.

Рассмотрим большие отрицательные

Согласно неопределённостей соотношениям, переход в адроны или кварки в этом случае возможен лишь на короткое время Поскольку теперь речь идёт о физике малых расстояний, то амплитуду диссоциации фотона в кварки при больших можно вычислить аналитически, пользуясь возмущений теорией по малой эфф. константе взаимодействий КХД. Вычисляя эти же величины с помощью дисперсионных соотношений, получаем П. с. для сечений аннигиляции в адроны. Посколькуможно менять непрерывно, то возникает непрерывное семейство П. с. Существуют разные формы записи подобных П. с. В качестве примера приведём П. с. для аннигиляции е ⁺ е ^- в адроны с полным изотопич. спином I = 1, полученные А. И. Вайнштейном, В. И. Захаровым, М. А. Шифманом (1978):

где "..." означает члены более высокого порядка по чем выписанные явно; - произвольный параметр; разумно выбирать не менее той величины, при к-рой члены становятся сравнимы с единицей; s - квадрат энергии в системе центра инерции - полное сечение аннигиляции в адроны с I = 1 в единицах сечения -константа сильного взаимодействия; - напряжённость глюонного поля (а - индекс цвета, а= 1,...,8); вакуумное среднееимеет смысл интенсивности непертурбативных (не описываемых в рамках теории возмущений) вакуумных полей; q- поле лёгкого кварка, q = и, d. В отличие от, вакуумный конденсат кварковых полей , к-рый также входит в (6), был введён в рассмотрение ранее в связи со спонтанным нарушением киральной симметрии.

Отметим, что в пределе из соотношения (6) следует при . С др. стороны, если брать возможно меньшие значения , то из-за обрезающего фактора интеграл от сечения насыщается при относительно небольших s. Продвижение в область малых ограничивается требованием законности отбрасывания в правой части (6) членов след. порядка по . Численный анализ показывает возможность выбора таких малых , что интеграл от сечения на 90% насыщается вкладом одного -мезона. Так возникает эфф. теория одного отд. резонанса в КХД.

Лит.: Бете Г., Солпитер Э., Квантовая механика атомов с одним и двумя электронами, пер. с англ., М., 1960; Bernstein J., Elementary particles and their currents, S. F.- L., 1968, ch. 12; Nоvikоv V. А. и др.. Charmonium and gluons, "Phys. Repts", 1978, v. 41C, Ml 1. В. И. Захаров,

Правила сумм в статистич. физике. Основой вывода и применения П. с. в этом случае являются спектральные представления двухвременных корреляц. ф-ций (см. Грина функция в статистич. физике)

Здесь - операторы в Гейзенберга представ лении, <...> - обозначает усреднение по большому каноническому распределению Гибб-са, - статистич. оператор (Sp - символ суммы диагональных матричных элементов оператора), H - оператор Гамильтона, - хим. потенциал, N- оператор числа частиц. Спектральная плотность

обобщает соотношение (2) при получении П. с. для произвольной пары операторов динамич. переменных [,- собств. значения гамильтониана Н, соответствующие векторам состояния -) - дельта-функция].

Простейшие П. с. получаются из (7) при

Дифференцируя h раз по f (или ) и полагая ,

можно получить бесконечный набор П. с.

выражающих моменты спектральной плотности через одноврем. корреляц. ф-ции. Правые части этих соотношений вычисляются точно, т. к. где = 1, тогда представляет собой n -кратный коммутатор. Выражение (9) используется для прак-тич. построения спектральной плотности в виде разложения по моментам, а также проверки корректности аппроксимаций П. с. эффективно служит для описания свойств обобщённой восприимчивости системы для к-рой справедливо спектральное представление

где в соответствии с принципом причинности. Ф-ция (10) описывает линейную реакцию системы на обобщённое внеш. поле, зависящее от координаты и времени t и характеризующееся частотой и волновым вектором k. Применение асимптотич. разложения даёт выражение для ВЧ-восприимчивости

где для моментов существуют П. с., аналогичные (9):

Из спектрального представления (10) следует формулировка флуктуационно-дисспативной теоремы, являющейся обобщением Крамерса- Крониеа соотношений на случай конечных темп-р и связывающей действительную и мнимую части обобщённой восприимчивости:

где P - символ гл. значения интеграла, поэтому

Статич. предел (= 0) даёт П. с. для неоднородной восприимчивости

В однородном пределе (k= 0,=0) могут быть получены термодинамические П. с. При величина является измеряемой на опыте адиабатической (при пост, энтропии S )восприимчивостью ( реакции функция), характеризующей изменение (реакцию) физ. величины (или оператора) А на действие постоянного и однородного внеш. поля, термодинамически сопряжённого внутр. параметру В. Для большинства эргодических физ. величин (см. Эргодическая гипотеза) совпадает с изотермич. восприимчивостью Величина пропорц. корреляционной ф-ции флуктуации А и В, совпадает со второй производной свободной энергии F по обобщённым полям, термодинамически сопряжённым А и В. Для эргодических систем согласование между динамич. и термоди-намич. свойствами обеспечивается П. с.

Наиб. распространённые примеры применения этого П. с.: магн. системы, где А = В =.- проекции вектора намагниченности на оси координат, - тензор магн. восприимчивости; проводники, где А= В=- проекции вектора плотности тока, =- тензор электропроводности; изотропные газы и жидкости, где А= В =- плотность частиц, внеш. поле - давление,= - сжимаемость, определяемая флуктуациями числа частиц; любые физ. системы, где А = В =- энергия системы, роль внеш. поля играет обратная темп-ра,

- теплоёмкость, определяемая флуктуациями энергии.

В случае, когда один или оба локальных оператора являются плотностями интегралов движения [напр.,= const], П. с. (12) принимает простой вид:

где , - фурье-компоненты В к А, причём

Спектральная плотность в пределе обладает дельтаобразной особенностью (т. н. центральный пик):

Как видно из (8), для этого необходимо вырождение системы (т. е. при ).

Приведённые П. с. применяются при анализе прямых экспериментов по измерению спектральной плотности для рассеяния электронов А = В =- плотность заряда; для нейтронов А = В = n- плотность частиц при потенциальном рассеянии и А=, В =.. при магн. рассеянии; для рассеяния света А = В =- проекции вектора поляризации среды.

П. с. весьма существенны при доказательстве и практич. применении теорем квантовой статистич. механики - Боголюбова теоремы и Голдстоуна теоремы, отражающих глобальные свойства симметрии системы. Эти теоремы наряду с П. с. используются при рассмотрении гидродинамики простой и сверхтекучей жидкости, сверхпроводимости, жидких кристаллов, спиновых волн в магнетиках и т. п.

Лит.: Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Боголюбовы. Н. (мл.). Садовников Б. И., Некоторые вопросы статистической механики, М., 1975; Форстер Д., Гидродинамические флуктуации, нарушенная симметрия и корреляционные функции, пер. с англ., М., 1980. Ю. Г. Рудой.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.