ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ

       

один из осн. законов термодинамики; устанавливает необратимость макроскопич. процессов, протекающих с конечной скоростью: процессы, связанные с теплообменом при конечной разности темп-р, с трением, с диффузией, с выделением джоулевой теплоты и др., текущими с конечной скоростью, необратимы, т. е. могут самопроизвольно протекать только в одном направлении.

Исторически В. н. т. возникло из анализа работы тепловых машин (франц. учёный С. Карно, 1824). Существует неск. эквивалентных формулировок В. н. т. Само название «В. н. т.» и исторически первая его формулировка (1850) принадлежат нем. учёному Р. Клаузиусу: невозможен процесс, при к-ром теплота переходила бы самопроизвольно от холодных тел к телам нагретым. При этом самопроизвольный переход не следует понимать в узком смысле: невозможен не только непосредств. переход, его невозможно осуществить и при помощи машин или приборов без того, чтобы в природе не произошли ещё к.-л. изменения (механич., тепловые и т. д.). Иными словами, невозможно провести процесс, единственным следствием к-рого был бы переход теплоты от холодного тела к нагретому. Если бы (в нарушение положения Клаузиуса) такой процесс оказался реально осуществимым, то можно было бы, разделив один тепловой резервуар на две части и переводя теплоту из одной части в другую, получить два резервуара с разл. темп-рами. Это позволило бы многократно осуществить с этими резервуарами Карно цикл и получить механич. работу при помощи периодически действующей (т. <е. в конце каждого цикла возвращающейся к исходному состоянию) машины за счёт внутренней энергии одного теплового резервуара. Поскольку это невозможно, в природе невозможны процессы, единств. следствием к-рых было бы совершение механич. работы, произведённой в результате охлаждения теплового резервуара (формулировка англ. физика У. Томсона, 1851). Обратно, если бы можно было получить механич. работу за счёт внутр. энергии одного теплового резервуара (в противоречии с В. н. т., по Томсону), то можно было бы нарушить и положение Клаузиуса. Механич. работу, полученную за счёт теплоты от более холодного резервуара, можно было бы использовать для нагревания более тёплого резервуара (напр., трением) и тем самым осуществить переход теплоты от холодного тела к нагретому без изменения состояния к.-л. иных тел.

В реальных тепловых двигателях процесс превращения теплоты в работу обязательно сопряжён с передачей определ. кол-ва теплоты внеш. среде. В результате тепловой резервуар двигателя охлаждается, а более холодная внеш. среда нагревается, что находится в согласии с В. н. т. Нарушение В. н. т. означало бы возможность создания т. н. вечного двигателя 2-го рода, совершающего работу за счёт внутр. энергии теплового резервуара и не изменяющего термодинамич. состояния окружающих тел. Следовательно, В. н. т. можно формулировать и как невозможность создания вечного двигателя 2-го рода (нем. физик В. Оствальд, 1888). -Г. А. Зисман. В совр. термодинамике В. н. т. формулируется как закон возрастания энтропии S. Согласно этому закону, в замкнутой макроскопич. системе энтропия при любом реальном процессе либо возрастает, либо остаётся неизменной, т. е. изменение энтропии dS?0 (равенство имеет место для обратимых процессов). В состоянии равновесия энтропия замкнутой системы достигает максимума и никакие макроскопич. процессы в такой системе, согласно В. н. т., невозможны. Приведённые в начале статьи формулировки В. н. т. представляют собой частные выражения общего закона возрастания энтропии.

Для незамкнутой системы направление возможных процессов, а также условия равновесия могут быть выведены из закона возрастания энтропии, применённого к составной замкнутой системе, получаемой путём присоединения всех тел, участвующих в процессе. Это приводит в общем случае необратимых процессов к неравенствам: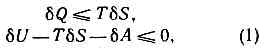

где dQ — переданное системе кол-во теплоты, dА — совершённая над ней работа, dU — изменение её внутр. энергии; знак равенства относится к обратимым процессам.

Важные следствия даёт применение В. н. т. к системам, находящимся в фиксированных внеш. условиях. Напр., для систем с фиксированной темп-рой и объёмом неравенство (1) приобретает вид: F?0, где F=U-TS— свободная энергия системы (Гельмгольца анергия). Т. о., в этих условиях направление реальных процессов определяется убыванием F, а состояние равновесия — минимумом этой величины (см. ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ).

В. н. т., несмотря на свою общность, не имеет абс. хар-ра, и отклонения от него (флуктуации) явл. вполне закономерными. Примерами флуктуац. процессов могут служить: броуновское движение ч-ц, равновесное тепловое излучение нагретых тел (в т. <ч. радиошумы), возникновение зародышей новой фазы при фазовых превращениях, самопроизвольные флуктуации темп-ры и давления в равновесной системе и т. д.

Статистическая физика, построенная на анализе микроскопич. механизма явлений, происходящих в макроскопич. телах, и выяснившая физ. сущность энтропии, позволила понять природу В. н. т., определить пределы его применимости и устранить кажущееся противоречие между механич. обратимостью любого, сколь угодно сложного, микроскопич. процесса и термодинамич. необратимостью процессов в макротелах. Как показывает статистич. термодинамика (австр. физик Л. Больцман, амер. физик Дж. У. Гиббс), энтропия системы связана со статистическим весом Р макроскопич. состояния: S=klnP. Статистич. вес Р пропорц. числу разл. микроскопич. реализаций данного состояния макроскопич. системы (напр., разл. распределений значений координат и импульсов молекул газа, отвечающих определ. значениям энергии, давления и др. термодинамич. параметров газа). Для замкнутой системы вероятность термодинамическая W данного макросостояния пропорц. его статистич. весу и определяется энтропией системы:

W = exp (S/k), или S=klnW. (2)

Т. о., закон возрастания энтропии имеет статистически-вероятностный хар-р и выражает пост. тенденцию системы к переходу в более вероятное состояние. Максимально вероятным явл. состояние равновесия; за достаточно большой промежуток времени любая замкнутая система достигает этого состояния.

Энтропия — величина аддитивная, она пропорц. числу ч-ц в системе. Поэтому для систем с большим числом ч-ц даже самое ничтожное относит. изменение энтропии, приходящейся на одну ч-цу, существенно меняет её абс. величину; изменение же энтропии, стоящей в показателе экспоненты в ур-нии (2), приводит к изменению вероятности W данного макросостояния в огромное число раз. Именно этот факт явл. причиной того, что для системы с большим числом ч-ц следствия В. н. т. практически имеют не вероятностный, а достоверный хар-р. Крайне маловероятные процессы, сопровождающиеся сколько-нибудь заметными уменьшениями энтропии, требуют столь огромных времён ожидания, что их реализация практически невозможна. В то же время малые части системы, содержащие небольшое число ч-ц, испытывают непрерывные флуктуации, сопровождающиеся лишь небольшим абс. изменением энтропии. Ср. значения частоты и величины этих флуктуации явл. таким же достоверным следствием статистич. термодинамики, как и само В. н. т.

Буквальное применение В. н. т. к Вселенной как целому привело Клаузиуса к неправомерному выводу о неизбежности «тепловой смерти» Вселенной.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.