- ВТОРОЙ ЗВУК
- ВТОРОЙ ЗВУК
-
слабозатухающие температурные волны, распространяющиеся в сверхтекучем жидком гелии (Не II) наряду с обычными звук. волнами (см. СВЕРХТЕКУЧЕСТЬ). Экспериментально В. з. был обнаружен В. П. Пешковым (1944). При распространении обычного звука в в-ве происходят колебания давления и плотности. Согласно двухкомпонентной модели сверхтекучего гелия Л. Д. Ландау, норм. и сверхтекучая компоненты при обычных звук. колебаниях ведут себя как единое целое, однако при В. з. они движутся различно — в местах сгущения норм. компоненты происходит разрежение сверхтекучей, и наоборот (колебаний плотности в в-ве не наблюдается). Относительные колебания сверхтекучей и норм. компонент проявляются в колебаниях темп-ры, т. к. лишь норм. компонента (газ возбуждений) участвует в переносе теплоты. Следовательно, скорость В. з. можно рассматривать как скорость звука в газе возбуждений (см. КВАНТОВАЯ ЖИДКОСТЬ). Вблизи абс. нуля темп-ры скорость с2 В. з. и скорость с обычного звука связаны соотношением с2=с/?3. В точке фазового перехода Не II в Не I (в l-точке) с2 обращается в нуль. Излучение В. з. производится нагревателем с колеблющейся темп-рой, а обнаружение В. з.—чувствит. термометром.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ВТОРОЙ ЗВУК
-
- слабозатухающие колебания темп-ры и энтропии в сверхтекучем гелии (HeII, см. Гелий жидкий). Существование В. з. обусловлено появлением дополнит. степеней свободы в HeII в результате фазового перехода гелия в сверхтекучее состояние (см. Звук в сверхтекучем гелии); в обычных же средах температурные колебания затухают на расстояниях порядка длины волны. Скорость распространения В. з. u2 определяется из ур-ний гидродинамики сверхтекучей жидкости (в двухкомпонентной модели, см. Ландау теория сверхтекучести). Если пренебречь аномально малым для гелия коэф. теплового расширения, то в волне В. з . осциллируют только темп-pa T и энтропия S. а плотность r и давление р остаются постоянными. Распространение В. з. не сопровождается переносом вещества (поток вещества
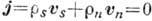 ), причём сверхтекучий и нормальный компоненты, имеющие плотности
), причём сверхтекучий и нормальный компоненты, имеющие плотности 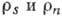 , колеблются со скоростями
, колеблются со скоростями 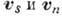 в противофазе относительно друг друга.
в противофазе относительно друг друга.
В. з. можно также интерпретировать как колебания концентрации квазичастиц в сверхтекучем гелии. В чистом 4He это колебания в системе ротонов и фононов, а в растворе 3He в HeII при низких темп-pax, когда число ротонов и фононов мало, это в осн. колебания концентрации примесных квазичастиц 3He, причём u2 существенно зависит от концентрации 3He в растворе. В точке перехода в сверхтекучее состояние (в
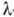 -точке) u2 обращается в нуль. Температурная зависимость
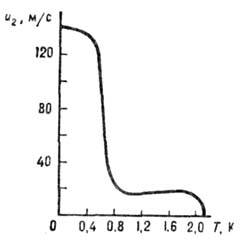
-точке) u2 обращается в нуль. Температурная зависимость 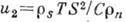 ( С - теплоёмкость гелия) для чистого 4He приведена на рис. При уменьшении темп-ры u2 стремится к предельному значению
( С - теплоёмкость гелия) для чистого 4He приведена на рис. При уменьшении темп-ры u2 стремится к предельному значению 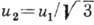 , где u1 - скорость первого (обычного) звука в гелии. В растворах 3He-HeII при низких темп-pax величина u2 близка (в меру малости концентрации 3He) к
, где u1 - скорость первого (обычного) звука в гелии. В растворах 3He-HeII при низких темп-pax величина u2 близка (в меру малости концентрации 3He) к 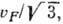 где
где 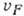 - фермиевская скорость в системе примесных квазичастиц 3He. В вырожденных растворах 3He-4He скорость В. з. растёт с ростом магн. поля и при полной поляризации ядерной спиновой системы 3He превосходит своё значение в отсутствие поля примерно в
- фермиевская скорость в системе примесных квазичастиц 3He. В вырожденных растворах 3He-4He скорость В. з. растёт с ростом магн. поля и при полной поляризации ядерной спиновой системы 3He превосходит своё значение в отсутствие поля примерно в 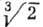 раза.
раза.
Вблизи поверхности Не II может распространяться поверхностный В. з., т. е. колебания в системе поверхностных квазичастиц сверхтекучего гелия (т. н. рип-плонов).
В растворе 3He-Не II атомы 3He притягиваются к поверхности Не II и образуют связанную с поверхностью систему двумерных поверхностных квазичастиц. Наблюдавшийся в растворе 3He-He II поверхностный В. з. представляет собой колебания концентрации поверхностных примесных квазичастиц 3He.
По аналогии с В. з. в сверхтекучем гелии В. з. иногда называют также и колебания концентрации в газе др. квазичастиц, напр. в газе фононов твёрдого тела.
Существование В. з. и скорость его распространения предсказали независимо Л. Д. Ландау (1941) и Л. Тиса (L. Tisza, 1938), метод генерации В. з. предложен E. M. Лифшицем (1944). В. з. в Не II был экспериментально обнаружен В. П. Пешковым (1944). Поверхностный В. з., предсказанный А. Ф. Андреевым и Д. А. Компанейцем (1972), был наблюдён в растворе 3 Не-Не II амер. учёными в 1974.
Лит. см. при ст. Звук в сверхтекучем гелии.
А. Э. Мейерович.
Реальные газы. При повышении плотности Г. его свойства перестают быть идеальными, столкновительные процессы играют все большую роль и размерами молекул и их взаимодействием уже нельзя пренебречь. Такой Г. наз. реальным (неидеальным). Размеры молекул являются одной из осн. характеристик неидеальных Г. С радиусами поперечного сечения
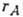 и
и 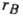 молекул типа А и В связаны поперечное сечение а рассеяния этих молекул друг на друге
молекул типа А и В связаны поперечное сечение а рассеяния этих молекул друг на друге

и длины свободного пробега l. Ф-ция распределения для l имеет вид:
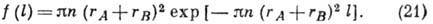
Cp. длина свободного пробега нек-рой молекулы А в газе частиц В, концентрация к-рых п, определяется ф-лой:
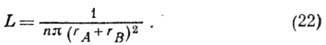
Ур-ние состояния неидеального Г.- ур-ние Ван-дер-Ваальса - имеет вид
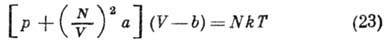
и учитывает как объем молекул (b - учетверенный собств. объем всех молекул Г., находящегося в объеме V,- т. <н. запрещенный объем), так и их притяжение между ними (постоянная а). Ур-ние (23) позволяет в условиях критич. состояния определить диаметр молекул Г.:

В Г., подчиняющемся уравнению Ван-дер-Ваальса, внутренняя энергия Г. начинает зависеть от его удельного объема:
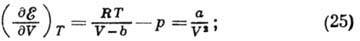
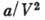 наз. внутр. давлением Г. Размеры молекул в Г., т. н. газокинетич. радиусы, связаны с характерными расстояниями, на к-рых проявляются силы межатомных и межмолекулярных взаимодействий. Кроме ур-ния Ван-дер-Ваальса для их определения используют эксперименты по рассеянию молекулярных пучков, а также зависимость вязкости и диффузии Г. от размеров частиц.
наз. внутр. давлением Г. Размеры молекул в Г., т. н. газокинетич. радиусы, связаны с характерными расстояниями, на к-рых проявляются силы межатомных и межмолекулярных взаимодействий. Кроме ур-ния Ван-дер-Ваальса для их определения используют эксперименты по рассеянию молекулярных пучков, а также зависимость вязкости и диффузии Г. от размеров частиц.
Фундам. свойством хаотичного движения, свойственного Г., является высокая степень "забываемости" предыдущих событий. Так, для полной релаксации (затухания) появившихся по тем или иным причинам отклонений энергии частиц от ср. тепловой необходимо лишь 1-2 столкновения для поступательно-поступательной релаксации, 4-5 - для вращательно-вращательной, 1020 - для колебательно-поступательной и, наконец, 1022 - для колебательно-колебательной релаксации. Строгое рассмотрение релаксационных процессов в индивидуальных Г. и особенно в смесях возможно только при наличии собств. размера частиц и требует решения систем интегрально-дифференц. кинетич. ур-ний Больцмана, в простейших случаях сводящихся к Эйнштейна - Фоккера - Планка уравнениям, диффузии уравнениям и т. д., решение к-рых возможно лишь на больших совр. ЭВМ.
Наиб. просто в теории Максвелла - Больцмана определяется время поступательно-поступательной релаксации
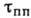 . Если в Г., состоящем из двух типов частиц, летящая частица А с массой т А сталкивается с покоящейся частицей В с массой т А, то
. Если в Г., состоящем из двух типов частиц, летящая частица А с массой т А сталкивается с покоящейся частицей В с массой т А, то
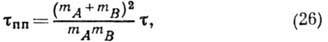
где
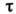 - время свободного пролёта частиц, зависящее от их диаметров. При т А = т В время
- время свободного пролёта частиц, зависящее от их диаметров. При т А = т В время 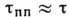 . В т. н. газе Лоренца, когда
. В т. н. газе Лоренца, когда 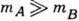 ,
, 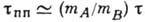 , в газе Рэлея (
, в газе Рэлея (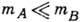 )
)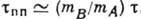 .
.
В реальном Г. появление неоднородности полей р и Т, а также макроскопич. потоков приводит к возникновению переноса массы - диффузии, потоки переноса энергии - к появлению теплопроводности и переноса импульса - вязкости. Гл. особенность кинетич. процессов переноса в Г. (в отличие от жидкостей и твёрдых тел) - его столкновительный механизм. Поэтому осн. характеристикой этих процессов в Г. является длина свободного пробега. Кинетич. свойства конкретного Г. определяются соответствующими феноменологич. коэф. С точностью до порядка величины коэф. диффузии D, температуропроводности
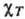 и кинематич. вязкости
и кинематич. вязкости 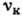 совпадают друг с другом, одинаково зависят от ср. скорости
совпадают друг с другом, одинаково зависят от ср. скорости 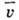 и длины свободного пробега:
и длины свободного пробега:
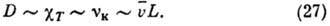
T. о., рассчитав L, напр., по ф-ле (22) при n=N0 и приняв для
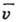 значение 104 см/с, получим для коэффициентов D,
значение 104 см/с, получим для коэффициентов D,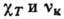 . значение, равное 10-1 см 2/с, что по порядку величины соответствует эксперим. данным.
. значение, равное 10-1 см 2/с, что по порядку величины соответствует эксперим. данным.
Коэф. D,
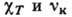 пропорциональны 1/n и
пропорциональны 1/n и 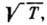 в то время как коэф. теплопроводности
в то время как коэф. теплопроводности 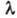 и коэф. сдвиговой вязкости
и коэф. сдвиговой вязкости 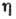 от n не зависят, и для разреженных Г. также
от n не зависят, и для разреженных Г. также 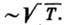 Для т. н. газа Кнудсена, в к-ром длина свободного пробега много больше характерных размеров сосуда,
Для т. н. газа Кнудсена, в к-ром длина свободного пробега много больше характерных размеров сосуда,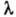 и
и 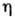 падают вместе с n; в этом случае процессы переноса имеют смысл только при взаимодействии Г. с поверхностью твёрдого тела или жидкости.
падают вместе с n; в этом случае процессы переноса имеют смысл только при взаимодействии Г. с поверхностью твёрдого тела или жидкости.
Т. <к.
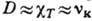 , то при одинаковых значениях характерного размера неоднородности (или дальности распространения этой неоднородности) время релаксации плотности, темп-ры или скорости перемещения будет примерно одинаковым:
, то при одинаковых значениях характерного размера неоднородности (или дальности распространения этой неоднородности) время релаксации плотности, темп-ры или скорости перемещения будет примерно одинаковым:

где K=D,
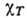 или
или 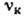 .
.
Более строгая теория переноса, основанная на рассмотрении систем кинетич. ур-ний, часто не допускает приведённой интерпретации с помощью длин свободного пробега, что объясняется необходимостью учёта (особенно при больших плотностях) сложного характера межмолекулярных взаимодействий, к-рые нельзя представлять как столкновение упругих шариков, и, кроме того, нарушением локального равновесия, что характерно, напр., для газа Кнудсена.
Рассмотрим условия равновесия системы, состоящей из двух сосудов с Г., соединённых друг с другом тонкой диафрагмой с отверстием; в сосудах поддерживаются разные темп-ры T1 и T2. Если длина свободного пробега L много меньше характерных размеров сосуда
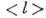 (число Кнудсена
(число Кнудсена 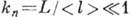 ), то условием равновесия будет равенство давлений в сосудах р 1= р 2, т. е.
), то условием равновесия будет равенство давлений в сосудах р 1= р 2, т. е. 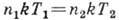 или
или

Т. <о., в этом случае плотность Г. выше в сосуде с более низкой темп-рой. В случае сильно разреженного Г., когда
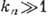 (газ Кнудсена), условием равновесия будет не равенство давлений, а равенство потоков, идущих из разных сосудов навстречу друг другу. Согласно (16), получим:
(газ Кнудсена), условием равновесия будет не равенство давлений, а равенство потоков, идущих из разных сосудов навстречу друг другу. Согласно (16), получим:

и, учитывая, что
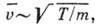
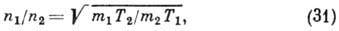
т. е. в условиях вакуума (во всяком случае, при
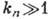 ) концентрация частиц в системе сообщающихся сосудов выше там, где выше темп-ра.
) концентрация частиц в системе сообщающихся сосудов выше там, где выше темп-ра.
Один из наиб. общих и обоснованных подходов к разработке ур-ния состояния реальных Г. основан на т. н. вириальном разложении по степеням V:
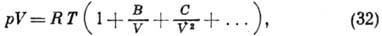
к-рое достаточно адекватно для состояний, удалённых от критич. точки. Вириальное разложение возможно также по степеням р:
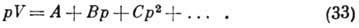
В ур-ниях (32) и (33) вириальные коэф. А, В и т. д. зависят только от темп-ры. При
 или
или  ур-ния (32) и (33) преобразуются в ур-ния состояния идеального Г.
ур-ния (32) и (33) преобразуются в ур-ния состояния идеального Г.
С межмолекулярным взаимодействием связано также изменение темп-ры реального Г. при протекании его с малой пост. скоростью через пористую перегородку (дросселировании, см. Джоуля - Томсона эффект). При этом в зависимости от условий может происходить охлаждение Г. и его нагрев; при т. н. темп-ре инверсии темп-pa сохраняется.
Внутр. строение молекул Г. слабо влияет на термич. свойства - давление, темп-ру, плотность - и на связь между ними. Существенное значение в первом приближении играет только молекулярная масса. Калорические свойства Г. (теплоёмкость, энтропия и др.), напротив, существенно зависят от строения молекул. От него также зависят и электрич., и магн. свойства Г. Так, для расчёта теплоёмкости Г. при пост. объёме ( с V )необходимо знать число внутр. степеней свободы молекул. Для точного расчёта калорич. свойств Г. нужно знать также уровни энергии молекул. Для идеального Г. мн. веществ калорич. параметры вычисляются с высокой точностью.
В Г. существенны два механизма поляризуемости молекул - деформационная и ориентационная поляризуемости. Электронные оболочки симметричных частиц, не имеющих собств. дипольного момента, во внеш. электрич. поле деформируются, в результате чего у них появляется дипольный момент в направлении поля. Поляризация газа из полярных молекул (т. е. молекул, обладающих собств. дипольным моментом) в электрич. поле сводится к появлению суммарного электрич. момента вдоль поля. Это явление наз. ориентационной поляризуемостью.
Г., состоящие из молекул, не обладающих собств. магн. моментом (напр., инертные Г., H2, CO2, H2O), диамагнитны. Если же молекулы имеют собств. магн. момент, то Г. во внеш. магн. поле ведут себя как парамагнетики.
Учёт межмолекулярного взаимодействия и внутр. строения молекул необходим при решении мн. проблем, напр. при исследовании влияния верх. разреженных слоев атмосферы на движение ракет и спутников Земли (см. Газовая динамика).
Свойства Г. элементарных частиц (электронного Г., фононного Г. и др.) изучает квантовая статистика.
Лит. Чепмен С., Каулинг Т., Математическая теория неоднородных газов, пер. с англ., M., 1960; Панченков Г. M., Лебедев В. II, Химическая кинетика и катализ, 2 изд., M., 1974; Гиршфельдер Дж., Кертисс Ч., Верд Р., Молекулярная теория газов и жидкостей пер. с англ., M., 1961; Кириллин В. А., Сычев В. В., Шейндлин А. Е., Техническая термодинамика, 4 изд M., 1983 Исихара А.. Статистическая физика, пер. с англ., М., 1973;Спроул Р., Современная физика, пер. с англ., М., 1974; Xир К., Статистическая механика, кинетическая теория и стохастические процессы, пер. с англ., M., 1976; Гордиец Б. Ф., Осипов А. И., Шелепин Л. А., Кинетические процессы в газах и молекулярные лазеры, M., 1980.
Ю. H. Любитов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
