- ПЕРЕСТАНОВОК ГРУППА
- ПЕРЕСТАНОВОК ГРУППА
-
степени n- множество S(n )перестановок п "предметов". П. г. такженаз. симметрической группой. Условимся считать, что данные предметы размещенына п занумерованных местах и символ
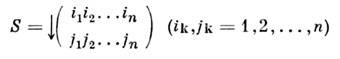
обозначает перестановку, к-рая состоитв перемещении предмета с места ik на место jk (движение вниз). Из этого представления видно, что порядок расположенияпар (ikjk) в символе S не имеетзначения, а умножение в группе S(n)
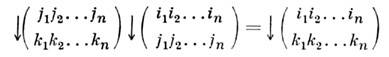
напоминает закон умножения матриц. П. г. <является конечной группой порядка n!
Элементы из S(n )могут быть порожденыболее простыми элементами, наз. циклами или транспозициями, напр.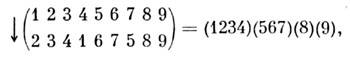
где каждый цикл (i1i2...im )определяется как частичная перестановка
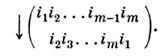
Цикл из двух символов наз. транспозицией. <Цикл можно записать иначе: (1234) = (2341) = (3412) = (4123); произведениенепересекающихся циклов коммутативно: (1234) (567) = (567) (1234); циклс одним символом обычно опускают. Любой цикл можно представить как произведениетранспозиций: (1234) = (12)(13)(14) (действие слева направо). Каждая перестановкапредставляется в виде произведения непересекающихся циклов (однозначно, <с точностью до порядка множителей). Каждая конечная группа порядка . изоморфна подгруппе группы S(n )(теорема Кэли).
Группа S(n )допускает точное линейноепредставление (см. Представление гриппы )в векторном пространстве Vn размерности п. Оператор представления Ts переводит х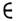
Vn в х'= Tsx
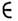Vn,так что в произвольном фиксиров. базисе е 1, е 2,...,е п представление Т s элемента S действует след. образом: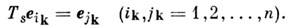
В каждом столбце и в каждой строке матрицы Ts содержится по единств. элементу, равному единице, <все остальные элементы равны нулю. Все неприводимые представления П. г. <можно описать при помощи Юнга схем.
Если физ. система состоит из п тождественныхчастиц, то группа симметрии её гамильтониана будет содержать группу S(п).Лит.: Любарский Г. Я., Теория группи ее применение в физике, М., 1958; Хамермеш М., Теория групп и ее применениек физическим проблемам, пер. с англ., М., 1966; Барут А., Рончка Р., Теорияпредставлений групп и ее приложения, пер. с англ., ч. 1 - 2, М., 1980.
С. И. Азакин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
