- МОТТОВСКИЕ ДИЭЛЕКТРИКИ
- МОТТОВСКИЕ ДИЭЛЕКТРИКИ
-
(диэлектрики Мот-та - Хаббарда) - кристаллы с диэлектрич. свойствами, происхождение к-рых связано не с влиянием пе-риодич. поля кристаллич. решётки (как в обычных диэлектриках или полупроводниках типа Ge и Si), а с сильным межэлектронным взаимодействием. Это состояние реализуется, если характерная энергия межэлектронного (кулоновского) взаимодействия U = е 2/
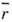 (
(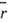 - ср. расстояние между электронами) больше ср. кинетич. энергии электронов, мерой к-рой является ширина разрешённой зоны
- ср. расстояние между электронами) больше ср. кинетич. энергии электронов, мерой к-рой является ширина разрешённой зоны 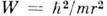 ( т - эффективная масса электрона). При U< W пригодна простая зонная диаграмма твёрдого тела (см. Зонная теория). Если U > W, то ситуация радикально изменяется. Зона может быть заполнена электронами частично, как в металлах, однако движению электронов, необходимому для переноса заряда, "мешают" др. электроны, находящиеся на соседних атомах. Своим отталкиванием они "запирают" (локализуют) каждый электрон на своём атоме и делают вещество диэлектриком. Это имеет место в системе, если
( т - эффективная масса электрона). При U< W пригодна простая зонная диаграмма твёрдого тела (см. Зонная теория). Если U > W, то ситуация радикально изменяется. Зона может быть заполнена электронами частично, как в металлах, однако движению электронов, необходимому для переноса заряда, "мешают" др. электроны, находящиеся на соседних атомах. Своим отталкиванием они "запирают" (локализуют) каждый электрон на своём атоме и делают вещество диэлектриком. Это имеет место в системе, если 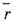 > а0, где a0 - боровский радиус. Более аккуратный анализ даёт критерий n1/3 a0
> а0, где a0 - боровский радиус. Более аккуратный анализ даёт критерий n1/3 a0 0,02, где n - концентрация электронов.
0,02, где n - концентрация электронов.При малой концентрации (n1/3 a0 < 0,02) в электро-нейтральной системе электроны и дырки образуют связанные состояния - экситоны и вещество, лишённое носителей заряда, оказывается непроводящим - диэлектриком. При большей концентрации (n1/3 а0> > 0,02) экранировка кулоновского взаимодействия приводит к исчезновению связанных состояний и происходит переход диэлектрик-металл ( переход Mотта, см. Переход металл - диэлектрик). В 1949 H. Ф. Мотт (N. F. Mott) объяснил переход кристалла из металлич. состояния в диэлектрическое при изменении давления и темп-ры уменьшением W.
Др. трактовка M. д. основана на использовании дискретной модели, описывающей электроны, перемещающиеся с узла j на узел i кристалла (с матричным элементом перехода t )при отталкивании двух электронов на одном узле (модель Хаббарда). Мерой кинетич. энергии электронов при этом также является ширина электронной зоны W =2zt, где z - число ближайших электронов-соседей. Если в системе имеется один электрон на узел (центр) (концентрация электронов n= N эл/N ат.= 1) и W> U, то вещество будет металлом с наполовину заполненной зоной. Однако при сильном взаимодействии (U > W )в осн. состоянии электроны локализованы на своих центрах и вещество оказывается M. д. Чтобы создать в такой системе подвижные носители заряда, надо "пересадить" электрон со "своего" узла на какой-то другой, на к-ром уже есть электрон; на это надо затратить энергию ~U, а выигрыш в энергии за счёт делокализации получающихся дырки и лишнего электрона порядка W, так что при U> W это невыгодно, н вещество остаётся диэлектриком со щелью ~(U - W )(щель Мотта - Хаббарда), хотя с точки зрения обычной зонной схемы оно было бы металлом.
Реально к M. д. принадлежат мн. соединения переходных и редкоземельных металлов с частично заполненными внутренними d - или f -оболочками. В силу малого радиуса d- и f -орбиталей их перекрытие и матричный элемент перехода малы, и для них легко выполняется условие U> W.
В фазе M. д. на центре имеются локализов. электроны, т. е. локализов. магн. моменты. Соответственно подобные вещества обычно обладают магн. упорядочением, как правило, они - антиферромагнетики. Магн. упорядочение в этом случае обусловлено т. н. косвенным обменным взаимодействием; оно возникает при частичной делокализации электронов - виртуальных переходах их на соседние (занятые) центры. Так описываются электронная структура и магн. свойства мн. соединений переходных металлов типа NiO. В непрерывной среде (без учёта периодич. потенциала решётки) состоянием, родственным M. д., является т. н. вигне-ровский кристалл, в к-ром электроны при малой плотности локализуются и образуют кристаллич. структуру с периодом, определяемым их плотностью.
При изменении внеш. условий (давления, темп-ры, состава соединения) в веществах, находящихся в фазе M. д., может произойти переход в металлич. состояние. Он может сопровождаться изменениями в кристаллич. структуре и исчезновением магн. упорядочения. Механизм перехода Мотта во многом ответствен за переход металл - диэлектрик в таких веществах, как V2O3, или в парах металлов.
Лит.: Мотт H. Ф., Переходы металл-изолятор, пер. с англ., M., 1979; Бугаев А. А., 3ахарченя Б. П., Чудновский F. А., Фазовый переход металл - полупроводник и его применение, Л., 1979; Хомский Д. И., Необычные электроны в кристаллах, M., 1987. Д. И. Хамский.
MOTTOBCKOE РАССЕЯНИЕ - рассеяние, обусловленное взаимодействием спина заряженной частицы с её орбитальным моментом, возникающим при движении в электрич. поле рассеивающего центра. Носит имя H. Ф. Мотта (N. F. Mott), разработавшего релятивистскую теорию рассеяния электронов. Характерной особенностью M. р. является его асимметрия относительно плоскости, содержащей спин и импульс электрона. Такая асимметрия используется для измерения поляризации электронов (см. ниже).
Рис. 1. Асимметрия моттовского рассеяния: вверху - траектории - электронов (поляризованных перпендикулярно плоскости чертежа), пролетающих слева и справа от кулоновского- центра- С; внизу-вависимость потенциальной энергии электронов
 от расстояния x до С. Сплошные линии соответствуют электростатической энергии; пунктир - полной энергии, включающей энергию спинорбитального взаимодействия.
от расстояния x до С. Сплошные линии соответствуют электростатической энергии; пунктир - полной энергии, включающей энергию спинорбитального взаимодействия.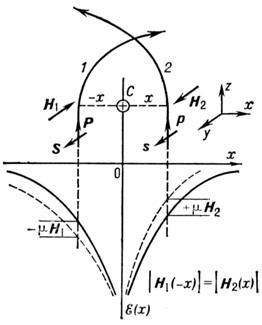
Пусть в системе покоя электронов, в к-рой определено направление их спинов, движется рассеивающий за-ряж. центр со скоростью u. Ток, соответствующий движению этого центра, создаёт магн. поле H = E.u/c, где E - напряжённость электрич. поля, создаваемого центром. T. о., в системе отсчёта, движущейся вместе с электроном, на его спин действует эфф. магн. поле, созданное током, т. е. рассеивающим заряж. центром. Это приводит к изменению энергии электрона на величину mH, где m - магн. момент электрона, связанный с его спином s: m = (e/mc)s (e, m - заряд и масса электрона).
Пусть две траектории электронов 1 и 2 проходят на мин. расстоянии x от положительно заряженного ку-лоновского центра С (рис. 1). В зависимости от того, слева ( х <0) или справа ( х >0) от центра проходит электрон, он рассеивается соответственно направо или налево. Если спин электронов направлен вдоль оси + у, их магн. момент m направлен вдоль - у (т. к. е <0). На спины электронов, движущихся слева и справа от кулонoвского центра, действуют противоположно направленные магн. поля, индуцированные относит. движением этого центра. Это приводит к разл. изменению потенц. энергии
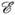 ( х )электронов на траекториях 1 и 2 (рис. 1). Для траектории 1 энергия спин-орбитального взаимодействия mH прибавляется к энергии
( х )электронов на траекториях 1 и 2 (рис. 1). Для траектории 1 энергия спин-орбитального взаимодействия mH прибавляется к энергии  ( х )эл.-статич. взаимодействия; для траектории 2 вычитается из
( х )эл.-статич. взаимодействия; для траектории 2 вычитается из 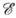 ( х). T. о., суммарная потенц. энергия оказывается нечётной ф-цией. При этом электронам, пролетающим слева от С, соответствует больший рассеивающий потенциал, чем для электронов, пролетающих на том же расстоянии справа от С. Различие в потенциалах приводит к увеличению интенсивности рассеяния вправо по сравнению с интенсивностью рассеяния влево. Очевидно, что при изменении ориентации спинов (или скоростей) на противоположную знак асимметрии изменится.
( х). T. о., суммарная потенц. энергия оказывается нечётной ф-цией. При этом электронам, пролетающим слева от С, соответствует больший рассеивающий потенциал, чем для электронов, пролетающих на том же расстоянии справа от С. Различие в потенциалах приводит к увеличению интенсивности рассеяния вправо по сравнению с интенсивностью рассеяния влево. Очевидно, что при изменении ориентации спинов (или скоростей) на противоположную знак асимметрии изменится.Асимметрия M. р. приводит к поляризации исходно неполяризов. электронов, рассеиваемых в заданном направлении. При этом поляризация электронов P = S(J)h, где h - единичный вектор вдоль нормали к плоскости рассеяния, включающей начальный p и конечный р' импульсы, J-угол между р и р', S(J)-т. н. ф-ция Шермана (рис. 2). Эта ф-ция определяет степень поляризации электронов: P = (п + - п_)/(п ++ п_), где n+ и п_ - числа электронов с противоположно направленными спинами. Направо рассеиваются преимущественно электроны со спинами, ориентированными вдоль оси +y, налево - вдоль - у[при этом величина S(J) для рассеянных налево и направо электронов составляет +S и -S]. Эта же ф-ция S(J) определяет
величину асимметрии рассеяния частично поляризованных вдоль h электронов: А= (N л.- N пр)/(N л+ +N пр). Здесь N л и N пр - числа электронов, рассеянных налево и направо. Зная S(J) по измеряемой величине А, анализируется поляризация электронов P; на этом принципе работает детектор Мотта. T. о., анализирующая и поляризующая способности M. р. характеризуются ф-цией Шермана. Зная S(J), можно определить поляризацию электронов (с энергией
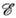 >=100 кэВ), рассеиваемых атомными ядрами на достаточно большие углы, когда можно пренебречь эффектами экранировки кулоновского барьера ядра. Величина S растёт с ростом заряда ядра, степень поляризации электронов, рассеянных на золоте, может достигать 40-50%.
>=100 кэВ), рассеиваемых атомными ядрами на достаточно большие углы, когда можно пренебречь эффектами экранировки кулоновского барьера ядра. Величина S растёт с ростом заряда ядра, степень поляризации электронов, рассеянных на золоте, может достигать 40-50%.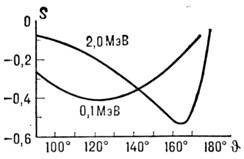
Рис. 2. Функция Шермана для золота при энергии электронов 0,1 Мэв и 2,о МэВ.
Детектор Мотта используется для калибровки др. поляризац. детекторов. Типичная схема эксперимента с детектором Мотта представлена на рис. 3. Если изме-ряется поляризация электронов с малой энергией, они предварительно ускоряются до энергии
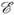 ~ 100 кэВ с помощью ускорителя 1 и после рассеяния под углом J = +120° на золотой фольге 2 регистрируются детекторами 3 и 4. Детектор Мотта использовался при исследовании несохранения чётности при бета-распаде ядер, к-рая приводит к возникновению продольной поляризации электронов (вдоль их импульса). T. к. детектор измеряет только поперечную поляризацию электронов, использовались дополнит. электрич. или магн. поля, обеспечивающие относит. разворот век- торов импульса и спина электронов.
~ 100 кэВ с помощью ускорителя 1 и после рассеяния под углом J = +120° на золотой фольге 2 регистрируются детекторами 3 и 4. Детектор Мотта использовался при исследовании несохранения чётности при бета-распаде ядер, к-рая приводит к возникновению продольной поляризации электронов (вдоль их импульса). T. к. детектор измеряет только поперечную поляризацию электронов, использовались дополнит. электрич. или магн. поля, обеспечивающие относит. разворот век- торов импульса и спина электронов.
Рис. 3. Схема детектора Мотта: 1- ускоритель; 2 - золотая фольга; 3, 4 - счётчики электронов.
Для исключения влияния многократного рассеяния электронов на меньшие углы при том же результирующем угле J необходимо использовать мишени с относительно небольшой плотностью атомов. Так, напр., плотность пучка атомов Hg (мишень) должна соответствовать давлению p < 10-3 мм рт. ст.; толщина золотой фольги, используемой в детекторах Мотта, не должна превышать 100 нм.
Лит.: Мотт H., Mесси Г., Теория атомных столкновений, пер. с англ., [3 изд.], M., 1969. В. Г. Флейшер.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
