КОЛЛЕКТИВНЫЕ ПЕРЕМЕННЫЕ

КОЛЛЕКТИВНЫЕ ПЕРЕМЕННЫЕ

- динамич. величины, описывающие такие бозевские возбуждения статистич. систем, к-рые представляют собой согласованное коллективное движение всех частиц системы. Коллективные возбуждения характерны для большинства статистич. систем (с большим числом N взаимодействующих друг с другем частиц). В ряде случаев отдельному такому возбуждению можно сопоставить волновой процесс, параметры к-рого определяют К. п. Наиб. наглядная реализация коллективного возбуждения системы - волна плотности числа частиц. Для оператора плотности числа частиц

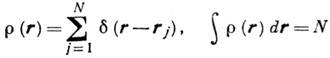
его фурье-компонента

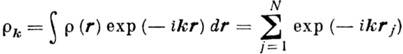
есть К. п., соответствующая волне плотности с волновым вектором k.

Такие гармонич. процессы являются возбуждениями бозевского типа. Описывающие их динамич. величины (в частности, 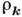) можно выбрать в качестве К. п., с помощью к-рых удаётся описать микроскопич. состояние системы, выразить в терминах К. п. операторы динамич. величин, относящихся ко всей системе, разработать приближенные методы расчёта осн. характеристик системы и т. д.

К. п. адекватно отражают структуру возбуждений системы в области длинных волн (по сравнению, напр., со ср. межатомным расстоянием, когда ещё можно говорить о волнах плотности). Поэтому они эффективны при описании тех свойств системы, к-рые связаны с учётом дальнодействующей части взаимодействия между частицами (особенно для систем с куло-новским взаимодействием). В ряде случаев гамильтониан взаимодействия Н ₁ целиком выражается в терминах К. п., напр.:

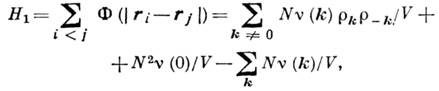
где Ф ( В) - потенциал взаимодействия, V- объём системы,

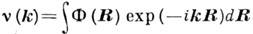
В общем случае при переходе к К. п. в гамильтониане выделяют части, выраженные через К. п. и через исходные индивидуальные переменные, а также смешанную часть, соответствующую взаимодействию коллективных возбуждений с возбуждениями отд. частиц. В первой части гамильтониана гл. роль играет квадратичная по К. п. форма, члены более высокого порядка интерпретируют как динамич. взаимодействие коллективных возбуждений.

Число К. п. и число оставшихся индивидуальных переменных, необходимых для описания микроскопич. состояния системы, должно равняться исходному числу степеней свободы. Учёт этого ограничения необходим при расчёте статистич. средних и статистич. суммы, часть к-рой может быть подсчитана с помощью переменных типа 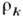, а часть ("коротковолновая") - с помощью исходных переменных.

Примеры К. п. в статистич. системах: а) В жидкостях К. п. соответствуют помимо плотности числа частиц 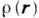ещё четыре величины: плотности импульса и энергии

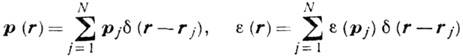
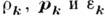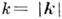Обычно рассматривают фурье-компоненты этих переменных, , к-рые в пределе переходят в интегралы движения: полное число частиц, полный импульс и полную энергию системы. При значениях волнового вектора , меньших обратного ср. расстояния между частицами, эти величины меняются достаточно медленно. Исследование ур-ний движения для этих К. п. и их корреляц. ф-ций является предметом молекулярной гидродинамики.

б) В твёрдом теле в гармонич. приближении микроскопич. состояние можно представить как суперпозицию нормальных колебаний всей системы, каждому из к-рых сопоставляется К. п. Это т. н. фононы.

в) В электронном газе с кулоновским взаимодействием К. п. являются величины 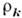, к-рые в нулевом приближении соответствуют плазменным колебаниям с ленгмюровской частотой (см. Плазма). Дальнейшее развитие метода связано с учётом взаимодействия К. п. с индивидуальными переменными. В случае, когда величина 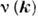конечна при k = 0, а также в случае, когда спектр индивидуальных возбуждений отделён от энергии осн. состояния конечной щелью (в сверхпроводниках), коллективные возбуждения при реализуются как акустич. колебания с частотой 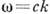. Колебания вырожденных ферми-жидкости или ферми-газа (т. н. нулевой звук )также являются коллективными возбуждениями.

г) В слабо неидеальном вырожденном бозе-газе аналогичная процедура введения К. п. приводит к появлению характерного спектра для зависимости энергии коллективного возбуждения 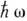от импульса :

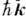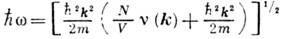
соответствующего при фононному спектру (Н. Н. Боголюбов, Д. Н. Зубарев, 1955).

д) В магнетиках низкоэнергетич. возбуждения реализуются в виде магнонов (колебаний магн. момента). К. п. (фурье-компоненты магн. момента) дают в нулевом приближении удовлетворит. описание осн. свойств магнетиков при низких (по сравнению с точкой Кюри) темп-рах.

е) К. н. используют и для описания коллективных эффектов в тяжёлых ядрах (объёмных колебаний и колебаний поверхности ядра, включая эффекты её несферичности).

Лит.: Б ом Д., Общая теория коллективных переменных, пер. с англ., М., 1964; X а а р Д. т е р, Введение в физику систем многих частиц, пер. с англ., М., 1961; Ю х н о в-с к и й И. Р., Головко М. Ф., Статистическая теория классических равновесных систем, К.. 1980; Boon J., V i p S., Molecular hydrodynamics, N. Y., 1980. Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.