- ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНЫХ ПОЛЕЙ
- ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНЫХ ПОЛЕЙ
-
- спец. случай дифракции (в оптике, радиофизике, акустике), когда падающая волна является частично когерентной (см. Когерентность). Флуктуации падающей волны приводят к аналогичным флуктуациям дифрагированной волны и влияют на её статистич. характеристики, такие как распределение ср. интенсивности, ср. диаграмма направленности, ср. размеры дифракц. пятен в фокусах линз и т. д. Если, напр., в оптич. системе регистрируются средние по времени величины, к-рые при наличии эргодичности совпадают со средними по статистическому ансамблю, то частичная когерентность падающей волны может изменять (как уменьшать, так и увеличивать) пределы разрешения такой системы.
Осн. черты Д. ч. к. п. наглядно видны на простейшем примере дифракции случайного монохроматич. поля u0 на отверстии S в плоском экране (рис.). Пусть ср. значение
и поле u0 в плоскости z=0 характеризуется ф-цией когерентности
(
- поперечная относительно z компонента 
- комплексное сопряжение). Выразив дифрагированное поле и при z>0 через и 0 в приближении Кирхгофа (см. Кирхгофа метод), для ср. интенсивности I дифрагированного поля вдали от отверстия получим:
Здесь
- длина волны, 
- единичный вектор, определяющий угловое распределение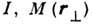 
- ф-ция пропускания отверстия, равная единице на S и нулю - вне S, и опущен медленно меняющийся коэф. пропорциональности.
В случае когерентной падающей волны, когда характерный размер отверстия а мал по сравнению с радиусом корреляции падающего поля l К[характерным масштабом спадания
], в ф-ле (*) 
, и ср. интенсивность равна
,
откуда видно, что угловое распределение I определяется формой отверстия S, как это имеет место при дифракции регулярной плоской волны. В противоположном предельном случае некогерентного освещения,
, можно пренебречь 
по сравнению с 
, тогда
где S - площадь отверстия. При этом угловое распределение I определяется ф-цией Г°, т. е. характером неоднородностей u0, и не зависит от формы отверстия. Поэтому если в отверстие поместить фокусирующую линзу с фокусным расстоянием F, то характерный размер фокального пятна будет в среднем равен
, а не 
, как в случае когерентного освещения. Корреляц. свойства излучения характеризуют степенью когерентности 
. В случае когерентной падающей волны 
= 1. Для частично когерентного освещения 
, при малых l К величина 
пропорциональна фурье-преобразованию от распределения интенсивности по отверстию S (см. Ван-Циттерта - Цернике теорема).
Лит.: Борн M., Вольф Э., Основы оптики, пер. с англ., 2 изд., M., 1973, гл. 10; Введение в статистическую радиофизику, ч. 2 - Рытов С. M., Кравцов Ю. А., Татарский В. И., Случайные поля, M., 1978, p 10, 11; Axманов С. А., Дьяков Ю. E., Чиркин А. С., Введение в статистическую радиофизику и оптику, M., 1981, гл. 4, p 5. Л. А. Апресян.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
