СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ

СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ
СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ

       
величина Z, обратная нормирующему множителю в каноническом распределении Гиббса в статистич. физике классич. систем и равная интегралу по всем фазовым переменным р, q системы:
СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ
где Н(р, q) — Гамильтона функции, системы, зависящая от всех координат q и импульсов р её ч-ц, N — число ч-ц. С. и. позволяет вычислить все потенциалы термодинамические классич. системы, когда можно пренебречь квант. эффектами. Напр., свободная энергия (Гельмгольца энергия) F=-kTlnZ. В квант. статистич. физике величине С. и. соответствует статистическая сумма.

Физический энциклопедический словарь. — М.: Советская энциклопедия. . 1983.

СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ

- величина, обратная нормирующему множителюв каноническом распределении Гиббса в статистич. физике классич. <систем и равная интегралу по всем фазовым переменным р, q системы:
8067-48.jpg

где H(p,q) - Гамильтона функция системы, N - число частиц, Т - абс. темп-pa. Для системы N частиц (без внутр. степенейсвободы), взаимодействующих с парным потенциалом 8067-49.jpg, ф-ция Гамильтона (полная энергия как ф-ция координат и импульсов всехчастиц)
8067-50.jpg

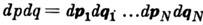8067-51.jpg - элементобъёма фазового пространства, множитель 1/N! связан с тождественностьючастиц, множитель 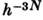8067-52.jpgсвязан с тем, что наим. размер ячейки в фазовом пространстве равен Л, еслирассматривать С. и. как предел статистической суммы при переходеот квантовой механики к классической. С. и. наз. также интегралом состояний.

С. и. связан со свободной энергией системы ( Гельмгольца энергией )соотношением 8067-53.jpg, к-рое является одним из основных в статистич. физике, т. к. позволяетвычислить F как ф-цию темп-ры, объёма и числа частиц в зависимостиот закона взаимодействия между частицами, а следовательно вычислить и др.потенциалы термодинамические.

Интегрирование по импульсам в С. и. легко выполняется, в результатеС. и. сводится к конфигурационному интегралу по 3N координатам:
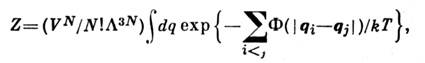
8067-54.jpg

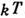где 8067-55.jpg- длина волны де Бройля, соответствующая энергии 8067-56.jpg.Для идеального газа 8067-57.jpg. В квантовой механике координаты и импульсы являются некоммутирующимиоператорами и подобное упрощение статистич. суммы невозможно. ВычислениеС. и.- одна из осн. задач статистич. физики классич. систем (см., напр., Вириальное разложение).

Лит.: Майер Д ж., Гепперт-Майер М., Статистическая механика, <пер. с англ., 2 изд., М., 1980, гл. 8; Хилл Т., Статистическая механика, <пер. с англ., М., 1960, гл. 5; Леонтович М. А., Введение в термодинамику. <Статистическая физика, М., 1983. Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ" в других словарях:

  • Функциональный интеграл — (континуальный интеграл, интеграл по траекториям, фейнмановский интеграл по траекториям)  запись или результат функционального интегрирования (интегрирования по траекториям). Находит наибольшее применение в квантовой физике (квантовой теории …   Википедия

  • Статистическая физика —         раздел физики, задача которого выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т.д.), через свойства этих частиц и взаимодействие между ними.… …   Большая советская энциклопедия

  • КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА — распределение вероятностей состояний статистического ансамбля систем, к рые находятся в тепловом равновесии со средой (термостатом) и могут обмениваться с ней энергией при пост. объёме и пост. числе ч ц (т. е. статистич. распределение для… …   Физическая энциклопедия

  • ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ — определённые функции объёма (V), давления (р), темп ры (Т), энтропии (S), числа ч ц системы (N) и др. макроскопич. параметров (xi), характеризующих состояние термодинамической системы. К П. т. относятся: внутренняя энергия U=U(S, V, N, xi),… …   Физическая энциклопедия

  • КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА — распределение вероятностей состояний статистич. ансамбля систем, к рые находятся в тепловом равновесии со средой (термостатом) и могут обмениваться с ней энергией при пост. объёме и пост. числе частиц; соответствует канонич. ансамблю Гиббса. К. р …   Физическая энциклопедия

  • Статистическая сумма —         величина, обратная нормирующему множителю канонического Гиббса распределения (См. Гиббса распределение) в квантовой статистической физике (См. Статистическая физика). В классической статистической физике такая величина называется… …   Большая советская энциклопедия

  • Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… …   Энциклопедия инвестора

  • СТАТИСТИЧЕСКАЯ ФИЗИКА — раздел физики, посвящённый изучению св в макроскопич. тел, т. е. систем, состоящих из очень большого числа одинаковых ч ц (молекул, атомов, эл нов и т. д.), исходя из св в этих ч ц и вз ствий между ними. Изучением макроскопич. тел занимаются и др …   Физическая энциклопедия

  • Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… …   Энциклопедия инвестора

  • ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… …   Словарь-справочник терминов нормативно-технической документации


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»