РАЗМЕРНОСТЕЙ АНАЛИЗ

РАЗМЕРНОСТЕЙ АНАЛИЗ

       

метод установления связи между физ. величинами, существенными для изучаемого явления, основанный на рассмотрении размерностей этих величин. В основе Р. а. лежит требование, согласно к-рому ур-ние, выражающее искомую связь, должно оставаться справедливым при любом изменении единиц входящих в него величин. Это требование совпадает с требованием равенства размерностей величин в левой и правой частях ур-ния. Ф-ла размерности к.-л. физ. .величины В имеет вид:

(В)=LlMmTt,или dimB=LlMmTt (1)

(dim от англ. dimension — размер, размерность). (В) — символ размерности определяемой (производной) физ. величины (обычно берётся в прямые скобки); L, М, Т, . . .— символы величин, принятых за основные (соответственно длины, массы, времени и т. д.); l, m, t, . . . — целые или дробные, положительные или отрицательные вещественные числа, наз. показателями размерности, или размерностью производной величины В. Так, ф-ла размерности для ускорения о записывается в виде (a)=LT-2, для силы — LMT-2. Понятие размерности распространяется и на осн. величины. Принимают, что размерность осн. величины в отношении самой себя равна единице и что от др. величин она не зависит; тогда ф-ла размерности осн. величины совпадает с её символом. Если единица производной величины не изменяется при изменении к.-л. из осн. единиц, то такая величина обладает нулевой размерностью по отношению к соответствующей основной. Так, ускорение обладает нулевой размерностью по отношению к массе. Величины, в размерности к-рых все осн. величины входят в нулевой степени, наз. безразмерными. Выбор числа физ. величин, принимаемых за основные, и самих этих величин в принципе произволен, но практич. соображения приводят к нек-рому ограничению свободы в выборе осн. величин и их единиц.

В СГС системе единиц за осн. величины принимают длину, массу и время. В этой системе размерность физ. величины выражается произведением трёх символов L, М и Т в соответствующих степенях. Международная система единиц (СИ) содержит семь осн. величин: кроме длины, массы и времени, силу тока (символ I), темп-ру (9), силу света (J), кол-во в-ва (N).

Если для исследуемого явления установлено, с какими величинами может быть связана искомая величина, но вид этой связи неизвестен, для её нахождения составляют ур-ние размерностей, в к-ром в левой части будет стоять символ искомой величины со своим показателем размерности, а в правой — произведение символов величин, от к-рых искомая величина зависит, но с неизвестными показателями размерности. Задача нахождения связи между физ. Величинами сводится в этом случае к отысканию значений соответствующих показателей размерности. Если, напр., требуется определить время т прохождения пути s телом массой m, движущимся поступательно и прямолинейно под действием пост. силы f, то можно составить ур-ние размерности, имеющее вид:

T=LxMy(LMT-2)z, (2)

где х, у, z неизвестны. Требование равенства показателей размерности левой и правой частей в ур-нии (2) приводит к системе ур-ний: x+z=0, y+z=0, -2z=1, откуда следует, что x=y=l/2, z=-1/2 и t=C?ms/f. (3)

Безразмерный коэфф. С, равный согласно законам механики ?2, в рамках Р. а. определить нельзя.

В этом состоит своеобразие Р. а. Устанавливаемая с его помощью зависимость искомой величины от величин, определяющих исследуемое явление, находится с точностью до пост. коэфф. Для получения точных количественных соотношений нужны дополнит. данные. Поэтому Р. а. не явл. универсальным методом. Он нашёл плодотворное применение в тех областях физики (гидравлике, аэродинамике и др.), где строгое решение задачи часто наталкивается на значит. трудности, в частности из-за большого числа параметров, определяющих физ. явление. При решении сложных задач на основе Р. а. большую роль сыграла теорема (её наз. p-теоремой), согласно к-рой всякое соотношение между нек-рым числом размерных величин, характеризующих данное физ. явление, можно представить в виде соотношения между меньшим числом безразмерных комбинаций, составленных из этих величин. Эта теорема связывает Р. а. с теорией физ. подобия, в основе к-рой лежит утверждение, что если все соответствующие безразмерные характеристики (подобиякритерии) для двух явлений одинаковы, то эти явления физически подобны (см. ПОДОБИЯ ТЕОРИЯ).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

РАЗМЕРНОСТЕЙ АНАЛИЗ

- метод установления связи между физ. величинами, существенными для изучаемого явления, основанный на рассмотрении размерностей единиц этих величин.

В основе Р. а. лежит требование: ур-ние, выражающее искомую связь, должно оставаться справедливым при любом изменении единиц входящих в него величин. Если это требование выполняется, то размерности в левой и правой частях ур-ния совпадают; если этого не происходит, то изменение к.-л. физ. величины вызовет разные изменения в обеих частях ур-ния и равенство нарушится. Неравенство размерностей левой и правой частей ур-ния может означать, что не учтена к.-л. величина, существенная для данного явления, либо в ур-ние должна входить неучтённая размерная константа. Напр., ур-ние для периода колебаний матем. маятника, длина к-рого l и масса т, можно записать в виде

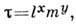
а для размерностей оно будет иметь вид

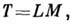
т. е. для размерностей равенство не выполняется. Однако известно, что колебания маятника происходят под действием силы тяжести, т. е. в ур-ние для т нужно ввести ускорение свободного падения g:

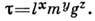
Тогда для размерностей получим

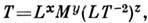
а для показателей размерностей - систему ур-ний

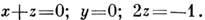
Т. е. z = -¹/₂, x= ¹/₂, у =0. И искомое ур-ние имеет вид

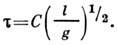
Безразмерный коэф. С, равный, согласно законам механики, 2p, методом Р. а. определить нельзя. Т. о., ур-ния связи между физ. величинами устанавливаются методом Р. а. с точностью до пост. коэффициентов. Поэтому Р. а. не является универсальным, однако он нашёл применение в гидравлике, аэродинамике и др. областях, где строгое решение задачи часто наталкивается на значит. трудности. При решении сложных задач на основе Р. а. используют т. н. p-теорему, согласно к-рой всякое соотношение между нек-рым числом размерных величин, характеризующих данное физ. явление, можно представить в виде соотношения между меньшим числом безразмерных комбинаций, составленных из этих величин. Эта теорема связывает Р. а. с теорией подобия, в основе к-рой лежит утверждение, что если все соответствующие безразмерные характеристики (подобия критерии )для двух явлений одинаковы, то эти явления физически подобны (см. Подобия теория).

Лит.: Бридшмен П. В., Анализ размерностей, пер. с англ., Л.- М., 1934; Седов Л. И., Методы подобия и размерности в механике, 10 изд., М., 1987; Коган Б. Ю., Размер-ность физической величины, М., 1968; Сена Л. А., Единицы физических величин и их размерности, 3 изд., M. 1989.

Л. А. Сена.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.