РАДИАЦИОННЫЕ ПОПРАВКИ

РАДИАЦИОННЫЕ ПОПРАВКИ

       

в квантовой электродинамике поправки к значениям нек-рых физ. величин и к сечениям разл. процессов (вычисленным по ф-лам релятивистской квант. механики), обусловленные вз-ствием заряж. ч-цы с собственным эл.-магн. полем. Р. п. рассчитывают по методу теории возмущений, представляя их в виде ряда по степеням постоянной тонкой структуры a=e2/ћnc»1/137 (где е — заряд эл-на), n-й член к-рого можно рассматривать как результат испускания и поглощения n виртуальных фотонов или электрон-позитронных пар. При вычислении Р. п. используется процедура перенормировки массы и заряда ч-цы.

Наибольший интерес представляют Р. п. к магн. моментам эл-на и мюона, к сверхтонкому расщеплению ат. уровней, радиац. смещение ат. уровней энергии (сдвиг уровней), Р. п. к сечениям рассеяния эл-на эл-ном или ат. ядром. Результаты расчётов Р. п. вплоть до величин 3-го порядка по степеням а блестяще согласуются с эксперим. данными и свидетельствуют о справедливости квант. электродинамики по крайней мере на расстояниях, больших 10-15 см. Р. п. растут с ростом энергии, и эфф. параметром разложения (эффективным зарядом) при высоких энергиях явл. величина a•ln(?/m), где ? — энергия ч-цы в системе центра инерции, m — её масса в энергетич. единицах.

Р. п. могут быть в ряде случаев подсчитаны не только для электродииамич. процессов, но и для процессов, вызванных др. вз-ствиями. Напр., в квантовой хромодинамике вычисляются Р. п. к сечениям глубоко неупругих процессов или к вероятностям распада мезонов со скрытым «очарованием».

При вычислении Р. п. к электродинамич. величинам с точностью выше 3-го порядка существ. вклад вносят процессы виртуального рождения адронов и эффекты слабого взаимодействия.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

РАДИАЦИОННЫЕ ПОПРАВКИ

- поправки возмущений теории к амплитудам разл. процессов в квантовой теории поля (КТП), обусловленные рождением и уничтожением виртуальных частиц.

Вычисление Р. п. к гл. эл.-динамич. процессам было первой задачей после построения осн. принципов кван-товой электродинамики (КЭД) в 30-х гг. Возникающие при расчётах бесконечности (см. Ультрафиолетовые расходимости )устраняются после перенормировок. Совр. метод вычисления Р. п. основан на применении релятивистски инвариантной теории возмущений, созданной в кон. 40-х гг. в работах Р. Фейнмана (R. Feyn-man), Дж. Швингера (J. Schwinger), С. Томонага (S. То-monaga). F. Дайсона (F. Dyson). Чаще всего используется наглядный метод Фейнмана диаграмм.

Исторически нач. импульс развитию совр. КТП дали опыты У. Лэмба (W. Lamb) и Р. Ризерфорда (R, Rether-ford) в 1947 по измерению расщепления и уровней атома водорода, вырожденных в релятивистской квантовой механике с учётом тонкого и сверхтонкого расщеплений. Оказалось, что в действительности вырождения нет - уровень на 1000 МГц ниже

Первые теоретич. расчёты были выполнены в том же году X. Бете (Н. Bethe). С полной последовательностью Р. п. учтены Н. Кроллом (N. Kroll) и У. Лэмбом, а также Дж Френчем (J. French) и В. Вайскопфом (V. Weis-skopf) в 1949 - после рождения совр. КЭД. Осн. вклад в это расщепление (лэмбовский сдвиг )вносит поправка к вершинной ф-ции; соответствующая диаграмма Фейнмана имеет вид, изображённый на рис. 1 (где сплошные линии отвечают электрону, волнистые - фотону).

Рис. 1.

Совр. теоретич. расчёты учитывают большое число диаграмм и приводят к величине расщепления =-=1057,910 МГц [Г. У. Эриксон (G. W. Erickson), 1971] или 1057,864(14) МгЦ [П. И. Mop (P. J. Mohr), 1975]. Кроме того, в расчётах учитывались эффекты следующих порядков по константе связи, были учтены также эффекты конечных размеров ядра. Эксперим. данные находятся в прекрасном согласии с теоретич. расчётами:= 1057,8514(19) МгЦ.

Вычисление вершинной диаграммы позволяет изучить ещё одну важную Р. п.- аномальный магнитный момент. Если принять магн. момент фермиона со спином вытекающий из теории Дирака, за единицу, то одно-петлевая Р. и. равна a/2p, где a ! 1/137 - постоянная тонкой структуры, константа связи КЭД. Эта поправка была вычислена впервые Дж. Швингером в 1948, а затем Р. Фейнманом в 1949 с помощью диаграммной техники. Обычно говорят не о самом магн. моменте, а о гиромагнитном отношени и g, определяемом как коэф. пропорциональности между магн. моментом m и спином S,m = g(e/2mc)S, где е., т- заряд и масса фермиона. В теории Дирака g= 2 и Р. п. описываются величиной (g - 2). Теоретич. расчёт позволяет учесть поправки порядка a⁴. При этом получаются разные значения для электрона и мюона, что связано с зависимостью результата от массы фермиона. Теоретич. результат для электрона:

эксперим. значение:

(по данным 1988).

Учёт поправок 4-го порядка по a потребовал вычисления почти 900 диаграмм Фейнмана. Для дальнейшего повышения точности необходимо учитывать поправки, связанные со слабым взаимодействием, вклад к-рых имеет порядок 10^-13.

При вычислении аномального магн. момента мюона необходимо учитывать, хотя и приближённо, поправки 4-го порядка по a (из-за большого фактора, пропорционального отношению масс мюона и электрона). Кроме этого, относительно велик вклад в величину (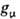- 2) адронных поправок из-за адронной перенормировки фотонного пропагатора. Чисто электродинамич. вклад есть

а адронная поправка равна 702(19) · 10^-10, так что полное теоретич. значение

находится в прекрасном согласии с эксперим. значением = 1165922(9)·10^-9. Оценка величины вклада слабого взаимодействия даёт 2·10^-9, что меньше точности и теории и эксперимента.

Ещё одна важная Р. п.- поправка к отношению сечений электрон-позитронной аннигиляции в адроны и мюоны:

Из квантовой хромодинамики (КХД) следует, что для этого отношения в области применимости теории возмущений осн. поправки связаны с обменами глюонами, в частности, гл. поправка определяется двухпетлэвой диаграммой (рис. 2) [спиральные линии здесь изображают глюоны, прямые - кварки, внешние (волнистые)

Рис. 2.

фотоны]. Вычислены вклады четырёхпетлевых диаграмм при условии малости масс кварков, так что окончат. выражение для Л имеет вид

где сумма берётся по всем типам кварков, Qi - величины кварковых зарядов (заряд электрона принят за единицу) и a_s - константа связи КХД.

Помимо процесса электрон-позитронной аннигиляции в адроны при высокой энергии, теория возмущений может применяться в КХД при изучении глубоко неупругих процессов, при этом вычисление Р. п. позволяет обнаружить логарифмич. отклонение от скейлинга Вьёркена (см. Масштабная инвариантность )в этих процессах.

В теории электрослабого взаимодействия Вайнбер-га - Глэшоу - Салама помимо вычисления Р. п. к наблюдаемым процессам, напр. к бета-распаду или распаду мюона, имеет смысл говорить также о вычислении поправок к осн. параметрам теории - к массам промежуточных векторных бозонов и Вайнберга углу, определяющему интенсивность нейтральных токов. Это связано с тем, что теория предсказывает определ. отношение между разными параметрами, к-рые измеряются в независимых экспериментах. Наиб. удобной параметризацией является следующая. Для угла Вайнберга q_W

где = 0,242(6) - значение, полученное из эксперим. данных но глубоко неупругому рассеянию в пренебрежении всеми Р. п. к заряженным (см. Заряженный ток )и нейтральным током, а DS - величина Р. п. Для массы f-кварка 45 ГэВ и массы Хиггса бозона100 ГэВ

= - 0,009(1). Для масс промежуточных векторных бозонов W^b, Z используется параметризация:

где = 37,281 ГэВ, - фермиевская константа слабого взаимодействия; величина d_W описывает вклад Р. п. в массы, возникающий при вычислении поправок к процессам глубоко неупругого рассеяния, к слабому распаду мюона (при определении G_F) и к поляризац. операторам фотона и промежуточных векторных бозонов. При упоминавшихся массах t -кварка и хиггсовского бозона теоретич. предсказание для величины d_W составляет

эксперим. значение:

Т. о., с уровнем достоверности 90% эксперим. данные подтверждают существование Р. п. к осн. соотношению для масс промежуточных векторных бозонов и угла смешивания Вайнберга.

Весьма существ. роль могут играть Р. п. и в разл. распадах. Напр., распады хиггсовских бозонов могут определяться однопетлевыми, а не древесными диаграммами, т. к. однопетлевые диаграммы в этом случае не малы, поскольку содержат большую константу связи хиггсовского бозона с тяжёлыми виртуальными кварками (b, t...). Также важна роль Р. п. в слабых радиац. распадах гиперонов типа и др.

Большой вклад в эти процессы вносят графики типа рис. 3 (где сплошная линия изображает барионы, волнистая линия - фотон, а штриховая - пион или каон).

Рис. 3.

Важность таких диаграмм связана с тем, что при интегрировании по импульсам виртуальных частиц в петле возникает большой логарифм , где М b,- массы бариона и пиона. Существует много и др. распадов, в к-рых Р. п. также чрезвычайно существенны.

Важна роль Р. п. и в моделях великого объединения теорий взаимодействия (GUT). В частности, в модели, осн. на группе SU(5), масса великого объединения в од-нопетлевом приближении не зависит от числа поколений фермионов, что связано с одинаковым вкладом в бета-функцию для разных зарядов. Однако на двух-петлевом уровне (т. е. при учёте Р. п. следующего за главным приближением) такая зависимость появляется. Кроме того, важна их роль и при получении синуса угла Вайнберга из модели великого объединения. Так, для SU(5)-модели учёт поправок изменяет затравочное значение квадрата синуса угла смешивания 0,237, следующее из теоретико-групповых свойств модели в нулевом приближении, на более близкое к эксперименту значение 0,228. Точнее,

при этом масса великого объединения M_GUT порядка 5·10¹⁵ ГэВ.

Помимо поправок в КЭД, КХД и теории электрослабого взаимодействия интерес представляет вычисление Р. п. в теории гравитации, однако пока этот вопрос не является строго поставленным, поскольку в квантовой теории гравитации, в отличие от теорий калибровочных полей, вычисление Р. п. невозможно - эта теория неперенормируема. Построение квантовой теории гравитации (в будущем) позволит однозначно вычислять квантовые поправки к любому процессу.

Лит.:Lеpa ge G. Р., Yеnnie D. R., The implications of QED theory for fundamental constants, в кн.: Proc. of the Second Intern. Confer, on precision measurement and fundamental constants, National Bureau of Standards, Gaithersbury, Waddison, 1982; Ициксон К., 3юбеr Ж.-Б., Квантовая теория поля, пер. с англ., т. 1, М., 1984; Kinoshita Т., Niziс В., Оkamоtо Y., Improved theory of the muon anomalous magne. tic moment, "Phys. Rev. Lett.", 1984, v. 52, №9, p. 717; Ama1-di U. и др., Comprehensive analysis of data pertaining to the weak neutral current and the intermediate - vector-bosson masses, "Phys. Rev.", 1987, v. 36 D, № 5, p. 1385; Gоrish-nу S. G., Кataev A. L., Lаrin S, A., Next-next-to-leading QCD correction to hadrons): analytical calculation and estimation of the parameter "Phys. Lett.",

1988, v. 212 B, № 2, p. 238; Kinoshita Т., Accuracy of the fine-structure constant, "IEEE Trans. Instrum. Meas.", 1989, v. 38, № 2, p. 172. Я. И. Коган,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.