- ПРЕЦЕССИЯ
- ПРЕЦЕССИЯ
-
(от позднелат. praecessio — движение впереди, предшествование), движение тв. тела, имеющего неподвижную точку О, к-рое слагается из вращения с угловой скоростью W вокруг оси Oz, неизменно связанной с телом, и вращения с угловой скоростью w вокруг оси Oz1 (рис.), гдеOx1,0yl,0zl —оси, условно наз. неподвижными, по отношению к к-рым рассматривается движение тела. ON — прямая, перпендикулярная к плоскости z1Oz, наз. линией узлов, y=x1ON— угол П. (см. ЭЙЛЕРОВЫ УГЛЫ). Наряду с П. тело совершает также нутационное движение, при к-ром происходит изменение угла нутации q=zlOz (см. НУТАЦИЯ).
Если во всё время движения q=const (нутация отсутствует) и величины W, w также остаются постоянными, то движение тела наз. р е г у л я р н о й П. Ось 0z описывает при этом вокруг оси П. Oz1 прямой круговой конус. Такую П. при произвольных начальных условиях совершает закреплённое в центре тяжести симметричное тело (гироскоп), на к-рое никакие силы, создающие момент относительно закреплённой точки, не действуют; осью П. в этом случае явл. неизменное направление кинетич. момента тела (см. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ). Симметричное тело, закреплённое в произвольной точке его оси симметрии и находящееся под действием силы тяжести (тяжёлый гироскоп или волчок), совершает при произвольных начальных условиях П. вокруг вертикальной оси, сопровождающуюся нутационными колебаниями, амплитуда и период к-рых тем меньше, а частота тем больше, чем больше угловая скорость собств. вращения W. Когда W->w, видимое движение гироскопа мало отличается от регулярной П.; такую П. наз. псевдорегулярной П. Угловая скорость псевдорегулярной П. тяжёлого гироскопа приближённо определяется равенством w=Pa/IW, где Р — вес гироскопа, а — расстояние от неподвижной точки до центра тяжести, I — момент инерции гироскопа относительно оси симметрии.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПРЕЦЕССИЯ
-
(от позднелат. praccessio - предшествование) - движение твёрдого тела, имеющего неподвижную точку О, к-рое определяется изменением угла прецессии
(см. Эйлера углы )и представляет собой вращение вокруг неподвижной оси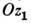 
с угл. скоростью П.
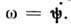Наряду с П. тело совершает собств. вращение с угл. скоростью 
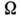вокруг неизменно связанной с телом оси 
(ось собств. вращения), а также нутационное движение, при к-ром происходит изменение угла нутации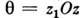
. (рис.). Если во всё время движения 
= const (нутация отсутствует) и величины 
также остаются постоянными, то движение тела наз. регулярной П. Ось 
описывает при этом вокруг оси П.
прямой круговой конус. Такую П. при произвольных нач. условиях совершает закреплённое в центре тяжести симметрич. тело (гироскоп), на к-рое никакие силы, создающие момент относительно закреплённой точки, не действуют; осью П. в этом случае является неизменное направление кинетич. момента тела (см. Момент количества движения). Симметрич. тело, закреплённое в произвольной точке оси симметрии и находящееся под действием силы тяжести (тяжёлый гироскоп или волчок), совершает при произвольных нач. условиях П. вокруг вертикальной оси, сопровождающуюся нутационными колебаниями, амплитуда и период к-рых тем меньше, чем больше угл. скорость собств. вращения 
Когда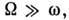 
видимое движение гироскопа мало отличается от регулярной П.; такую П., сопровождающуюся нутационными ВЧ-колебаниями малой амплитуды, наз. псевдорегулярной П. Угл. скорость псевдорегулярной П. тяжёлого гироскопа приближённо определяется равенством 
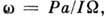где P - вес гироскопа, a - расстояние от неподвижной точки до центра тяжести, I- момент инерции гироскопа относительно оси симметрии. Сопротивление движению вызывает затухание нутационных колебаний, и П. постепенно становится регулярной. Движение широко применяемых в технике гироско-пич. систем носит характер псевдорегулярной П.; для изучения его используют обычно т. н. элементарную (прецессионную) теорию гироскопич. явлений. Подробнее см. в ст. Гироскоп. с. М. ТаргСхема прецессии твёрдого тела:
- неподвижные оси, по отношению к которым движется тело, ON- прямая, перпендикулярная к плоскости 
(линия узлов),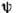
- угол 
ON.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
