МАТРИЦА ПЛОТНОСТИ

МАТРИЦА ПЛОТНОСТИ

       

(статистический оператор), оператор, при помощи к-рого можно вычислить ср. значение любой физ. величины в квант. статистич. механике и, в частном случае, в квант. механике. Термин «М. п.» связан с тем, что статистич. оператор задаётся обычно в виде матрицы rmn, строки и столбцы к-рой нумеруются индексами mn, отвечающими полному набору квант. чисел, описывающих состояние системы, а её диагональные элементы rmn определяют вероятности соответствующих состояний.

М. п. в квант. статистич. механике играет такую же роль, как ф-ция распределения в классич. статистич. механике.

В квант. механике состояние системы описывается волн. ф-цией y(x), соответствующей максимально полному набору данных о системе; такое состояние наз. ч и с т ы м с о с т о я н и е м. Ср. значение любой физ. величины ?, представляемой оператором ? , в состоянии, описываемом волн. ф-цией y(х), равно:

?=?y*(x)?(x)dx,

где интегрирование проводится по координатам всех ч-ц (для ч-ц со спином проводится, кроме того, суммирование по возможным значениям спина; y* — величина, комплексно сопряжённая y).

Вся квант. механика, за исключением нек-рых вопросов теории измерений, имеет дело с чистыми состояниями. В квант. статистич. механике состояние системы нельзя описать волн. ф-цией из-за отсутствия полной (максимально возможной) информации о квант.-механич. системе. Состояние, не основанное на полном (в смысле квант. механики) наборе данных о системе, в отличие от чистого наз. смешанным состоянием, или смесью состояний; такое состояние описывается М. п. rmn. Ср. значение любой физ. величины A , к-рой соответствует оператор ?, а в представлении квант. чисел m и n соответствует матрица Аnm, равно:

?=Sm,n rmnАnm.

Это усреднение включает как усреднение, связанное с вероятностным хар-ром квант. описания, так и статистич. усреднение, обусловленное неполнотой сведений о рассматриваемой системе, но эти операции не могут быть отделены друг от друга.

В частном случае М. п. может зависеть от координат ч-ц: r(х, х'), где х означает совокупность координат ч-ц x1, x2, ..., xN, а х' —совокупность x'1, х'2, ..., x'N (N — число ч-ц в системе), т. е. координаты ч-ц играют роль матричных индексов М. п. В координатном представлении М. п. связана с rmn соотношением

r(х, х') =Sm,n y*n(x')ym(x).

В этом представлении диагональные элементы М. п. r(х, х) определяют плотность вероятности в состоянии х. Для ч-ц со спином надо учитывать, кроме xi, также спиновые переменные. В Бозе — Эйнштейна статистике М. <п. симметрична относительно перестановок х1, х2,..., xN (или штрихованных переменных). Для ч-ц со спином вместе с координатами следует переставлять и спины.

В Ферми — Дирака статистике М. <п. антисимметрична.

В теории физ. измерений применение М. п. связано с тем, что квант. система, находящаяся до измерения в чистом состоянии, после измерения (в результате вз-ствия с измерит. прибором) будет находиться уже в смешанном состоянии.

М. п. удовлетворяет квант. ур-нию Лиувилля (или уравнению Неймана), к-рое определяет закон эволюции М. п. во времени и служит основой для неравновесной статистич. механики. Это ур-ние позволяет вычислить реакцию статистич. системы, находящейся в статистич. равновесии, на внешние возмущения (напр., на включение электрич. или магн. поля), а также построить статистич. операторы для систем, находящихся в неравновесном состоянии, когда имеются потоки частиц, энергии или импульса.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

МАТРИЦА ПЛОТНОСТИ

(статистический оператор) - оператор, при помощи к-рого можно вычислить ср. значение любой физ. величины в квантовой статистич. механике и, в частности, в квантовой механике. Термин "М. п." связан с тем, что статистич. оператор обычно задаётся в матричной форме и определяет плотность вероятности. M. п. введена Дж. фон Нейманом (J. von Neumann) и Л. Д. Ландау в 1927.

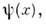В квантовой механике ср. значение физ. величины, представляемой оператором в квантовом состоянии, к-рое описывается волновой ф-цией равно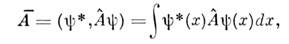

* означает комплексное сопряжение (для частиц со спином нужно учесть зависимость волновой ф-ции от спиновых переменных и, кроме интегрирования, выполнить суммирование по возможным значениям спина). Соответствующий статистич. ансамбль наз. чистым ансамблем, а состояние, к-рое можно описать волновой ф-цией,- "чистым" состоянием. Вся квантовая механика, за исключением нек-рых вопросов теории измерений, основана на применении чистых ансамблей.

Квантовая статистич. механика основана на использовании статистич. ансамбля более общего типа, а именно смешанного ансамбля (или смеси состояний), к-рый характеризуется заданием лишь вероятностей пребывания системы в разл. квантовых состояниях, описываемых волновыми ф-циями Для такого ансамбля ср. значение величины 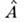определяется ф-лой

к-рую можно записать в виде

где Sp - след оператора, а - M. п. в х -представлении, c- совокупность одночастичных координат для частиц со спином включает спин s;. Матричный элемент оператора в x -представлении определяется соотношением

Чистое состояние есть частный случай смешанного, когда вероятность состояния равна 1, а вероятность остальных - нулю. В этом случае M. п. равна произведению волновых ф-ций

В общем случае M. п. нельзя представить в такой форме, преобразуя волновые ф-ции. Описание системы с помощью M. п. является неполным с точки зрения квантовой механики, т. к. оно не основано на максимально полном наборе данных, как при описании с помощью волновой ф-ции, но в статистич. механике эта "неполнота", как правило, не является недостатком. Полное описание системы очень большого числа частиц не только чрезвычайно сложно, но и излишне, поскольку для таких систем проявляются статистич. закономерности. Однако для осн. состояния квантовомеханич. систем с большим числом частиц иногда удаётся в нек-ром приближении теоретически рассчитать волновые ф-ции и пользоваться чистым ансамблем.

Физ. смысл M. п. можно пояснить, рассматривая подсистему с координатами c квантовомеханич. изо-лиров. системы с координатами к-рая описывается волновой ф-цией 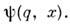Cp. значение величины

относящейся к подсистеме и зависящей лишь от х, равно

Определяя линейный оператор 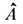в матричном координатном представлении с помощью соотношения

получаем для ср. значения оператора выражение

M. п. подсистемы 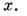Диагональные элементы M. п.

определяют вероятности координат подсистемы. T. о., состояние подсистемы описывается не волновой ф-цией, a M. п.

M. и. обладает след, свойствами: из нормировки вероятности вытекает, что M. п.- эрмитова, т. е.и, кроме того, симметрична относительно переменных 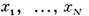(или включая спиновые переменные, для Базе- Эйнштейна статистики и антисимметрична для Ферми- Дирака статистики.

Если M. п. удовлетворяет условию 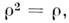то рассматриваемая система находится в чистом состоянии и обладает определ. волновой ф-цией. Действительно, когда 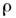приведено к диагональной форме, это означает, что к.-л. один из матричных элементов 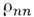равен 1, а остальные элементы равны нулю. Для любой физ. величины тогда имеем 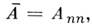что соответствует наличию определ. волновой ф-ции 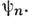В этом случае нет необходимости вводить M. п.

M. п. удовлетворяет квантовому ур-нию Лиувилля

аналогичному ур-нию Лиувилля в классич. статистич. механике. Это ур-ние получается из того факта, что удовлетворяет ур-нию Шрёдингера. В стационарном состоянии и 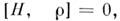т. е. M. п.- интеграл движения. Это свойство является исходным при построении равновесных статистич. ансамблей и перенесении идей Гиббса в квантовую статистику. Напр., для микроканонич. ансамбля при и вне этого интервала, где - собств. значение гамильтониана H. Для канонич. ансамбля

(F- своpодная энергия, или энергия Гельмголь-ца; T- абс. темп-pa). В этом случае

или, в матричной форме,

M. п. применяют в теории необратимых процессов. Если при система с гамильтонианом H находилась в состоянии статистич. равновесия, а затем адиабатически было включено внеш. возмущение H_t (напр., вызванное электрич. или магн. полем), зависящее от времени, то с помощью можно найти реакцию системы на внеш. возмущение. В линейном приближении по внеш. возмущению

- статистич. оператор в состоянии равновесия. Отсюда для ср. значения оператора получим

и операторы взяты в гейзенберговском представлении:

Эти ф-лы можно представить через двухвременные запаздывающие Грина функции, что используют в теории электропроводности и магн. резонанса.

M. п. применяют для построения операторов плотности комплексов молекул, удовлетворяющих цепочке Боголюбова уравнений, с помощью к-рой можно обосновать кинетич. ур-ние квантового газа.

M. п. используют в теории полярмзов. пучков частиц со спином (магн. моментом) или фотонов. Напр., M. п. пучка частиц со спином в смешанном состоянии имеет вид

- спиновые ф-ции двух разл. суперпозиций состояний M. п. в представлении спиновых ф-ций даётся выражением

где - i-я компонента поляризации, s_i.- матрицы Паули, е - единичная матрица. M. п. пучка фотонов с разл. поляризацией имеет аналогичный вид и зависит от трёх Стокса параметров, описывающих степени линейной и круговой поляризации относительно разл. осей.

Смешанный ансамбль частиц в разл. состояниях угл. момента описывается M. п. с элементами

Для того чтобы учесть симметрию, связанную с угл. моментом частиц ансамбля, удобно разложить r по неприводимым тензорным операторам угл. моментов

- Клебша- Гордана коэффициенты, К, Q- полный момент и его z-компонента,-

матрица, имеющая строк и столбцов.

Величины

наз. мультиполями состояния и характеризуют свойства поляризации и когерентности пучков. Три параметра (при с Q = наз. вектором ориентации и характеризуют средний по ансамблю угл. момент. Тензор 2-го ранга наз. тензором в n -строенности, он пропорционален ср. сферич. компонентам тензора электрич. квадрупольного момента.

Лит.: Ландау Л. Д., Лифшиц E. M., Квантовая механика, 4 изд., M., 1989, p4; их же, Статистическая физика, ч. 1, 3 изд., M., 1976, p 5; Mандельштам Л. И., Поли, собр. трудов, т. 5, M., 1950; Фон Нейман И., Математические основы квантовой механики, пер. с нем., M., 1964, гл. 5; Боголюбов H. H., Избр. труды, т. 2, К., 1970, с. 288; Зубарев Д. H., Неравновесная статистическая термодинамика, M., 1971, гл. 2-3; Александров И. В., Теория магнитной релаксации, M., 1975; Блум К., Теория матрицы плотности н ее приложения, пер. с англ., M., 1983.

Д. H. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.