- МАСШТАБНАЯ ИНВАРИАНТНОСТЬ
- МАСШТАБНАЯ ИНВАРИАНТНОСТЬ
-
(скейлинг), свойство неизменности ур-ний, описывающих к.-л. физ. процесс или явление, при одновременном изменении всех расстояний и отрезков времени в одно и то же число раз. (В квант. теории этому соответствует инвариантность относительно изменения импульса и энергии в одно и то же число раз.) Для этого необходимо, чтобы как в ур-ниях, так и в граничных условиях отсутствовали параметры, имеющие размерность длины или массы. На расстояниях, сравнимых с размерами атома, М. и. отсутствует (хотя она наблюдается для нек-рого класса макроскопич. физ. явлений, напр. в гидродинамике), но на расстояниях много меньших размеров адронов (=10-13 см) в сильном вз-ствии не обнаруживаются к.-л. параметры размерности длины и св-во М. и. кажется вполне возможным. В применении к процессам с реальными ч-цами, энергия ? и импульс р к-рых связаны соотношением ?2= m2c4+p2c2 (где m — масса покоя ч-цы), наличие размерного параметра та препятствует непосредств. проявлению М. и. Однако экспериментально установлено, что в нек-рых случаях зависимость сечений процессов при высоких энергиях (?-> mс2) от массы оказывается слабой и М. и. приближённо выполняется. Наиб. известные из таких процессов следующие.а) Глубоко неупругое лептон-адронное рассеяние, напр. e+h®е'+Х (где е, е' — начальный и конечный эл-н, h — начальный адрон, X — совокупность нерегистрируемых конечных адронов), безразмерные формфакторы к-рого вместо зависимости от двух импульсных переменных (квадрата переданного четырёхмерного импульса (4-импульса) q2=(ре-pе')2 и квадрата энергии системы X (в системе её центра инерции), M2Xс4= (pе-pe'+ph)3c2, где ре, ре', рh — 4-импульсы соответственно эл-на е, е' и адрона h) в области |q2|->1 (ГэВ/с)2 зависят только от их безразмерного отношения q2/M2Xc2 (т. н. скейлинг Бьёркена, названный по имени амер. физика Дж. Бьёркена; (см. ПАРТОНЫ)).Более точные измерения показывают, что эта М. и. справедлива лишь для не слишком большого интервала передач импульса. Отклонение от скейлинга в этом случае, как предполагают, связано с процессами вз-ствия кварков и глюонов, согласно законам квантовой хромодинамики.б) Инклюзивные адронные процессы а+b®c+Х, инвариантное сечение к-рого вместо зависимости от продольных по отношению к оси соударения компонент трёхмерных импульсов ра и рLс адронов а и с (в системе центра инерции) в области pа>pLс-> 1 ГэВ/с и малых поперечных импульсов, рTс <- 1 ГэВ/с, зависит только от их отношения (т. н. скейлинг Фейнмана, названный по имени амер. физика Р. Фейнмана). Эта М. и. также оказывается нарушенной для ч-ц, рождающихся с относительно малой энергией в системе центра инерции (т. н. область нионизации.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МАСШТАБНАЯ ИНВАРИАНТНОСТЬ
-
(скейлинг)- свойство неизменности ур-ний, описывающих нек-рую физ. теорию или к.-л. физ. процесс, при изменении всех расстояний и промежутков времени в одинаковое число раз. Такие изменения образуют группу масштабных преобразований (называемых также преобразованиями подобия), определяемую след, законом изменения координат пространства и времени:

где
 - числовой параметр преобразования, к-рый при
- числовой параметр преобразования, к-рый при  соответствует однородному растяжению, а при
соответствует однородному растяжению, а при  - однородному сжатию пространства времени в r раз. В релятивистской теории масштабное преобразование вместе с 10 преобразованиями группы Пуанкаре (см. Пространственно-временная симметрия )образует т. н. группу Вейля. Физ. величины изменяются при масштабном преобразовании в соответствии со своими размерностями, напр, вектор-потенциал эл.-магн. поля и ток преобразуются по законам
- однородному сжатию пространства времени в r раз. В релятивистской теории масштабное преобразование вместе с 10 преобразованиями группы Пуанкаре (см. Пространственно-временная симметрия )образует т. н. группу Вейля. Физ. величины изменяются при масштабном преобразовании в соответствии со своими размерностями, напр, вектор-потенциал эл.-магн. поля и ток преобразуются по законам 
Безразмерные величины, <а также такие величины, как массы частиц, при масштабном преобразовании не меняются.
M. и. (иногда наз. также подобием или автомодельностью по аналогии с теорией , фазовых переходов 2-го рода и гидродинамикой) обладает ряд ур-ний физ. теорий. Это происходит в тех случаях, когда в решение ур-ний не входят массы или другие размерные параметры, не меняющиеся при масштабном преобразовании. В классич. физике важным примером являются Максвелла уравнения, к-рые обладают M. и. для любых расстояний и промежутков времени. Клейна - Гордона уравнение и Дирака уравнение масштабно инвариантны для расстояний, малых по сравнению с ком-птоновской длиной волны соответствующих частиц, и промежутков времени, малых по сравнению с этой длиной, делённой на скорость света. Для расстояний, сравнимых с комптоновской длиной волны (и соответствующих промежутков времени), M. и. нарушается из-за наличия масс частиц. О такой ситуации говорят как о нарушенной M. и.
В физике элементарных частиц нарушенная M.и. обнаружена в поведении структурных функций, описывающих эксперименты по глубоко неупругим процессам рассеяния лептонов на адронах при высокой энергии. Для глубоко неупругого электрон-протонного рассеяния
 (где X обозначает совокупность адронов в конечном состоянии) при произвольных значениях энергии налетающего электрона следует ожидать зависимости структурных ф-ций по отдельности от двух имеющихся в задаче кинематич. переменных:
(где X обозначает совокупность адронов в конечном состоянии) при произвольных значениях энергии налетающего электрона следует ожидать зависимости структурных ф-ций по отдельности от двух имеющихся в задаче кинематич. переменных: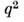 - квадрата 4-импульса q, переданного от электрона к протону, <и
- квадрата 4-импульса q, переданного от электрона к протону, <и 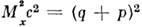 - квадрата энергии образующейся адронной системы X в системе её центра инерции; здесь r- 4-импульс нач. протона. Однако на ускорителе СЛАК в 1968 было впервые обнаружено, что при больших отрицат. значениях
- квадрата энергии образующейся адронной системы X в системе её центра инерции; здесь r- 4-импульс нач. протона. Однако на ускорителе СЛАК в 1968 было впервые обнаружено, что при больших отрицат. значениях 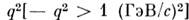 структурные ф-ции зависят только от одного безразмерного отношения -
структурные ф-ции зависят только от одного безразмерного отношения -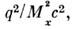 а не от
а не от  и
и 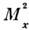 по отдельности. Такое поведение структурных ф-ций было теоретич. предсказано также в 1968 Дж. Бьёркеном (J. Bjorken) (скейлинг Бьёркена). Скейлинг Бьёркена нашёл естеств. объяснение в рамках пар-тонной модели адронов (см. Партоны).
по отдельности. Такое поведение структурных ф-ций было теоретич. предсказано также в 1968 Дж. Бьёркеном (J. Bjorken) (скейлинг Бьёркена). Скейлинг Бьёркена нашёл естеств. объяснение в рамках пар-тонной модели адронов (см. Партоны).Аналогично глубоко неупругим процессам M. и. наблюдается и в адрон-адронных столкновениях при высоких энергиях. Так, для адронных инклюзивных процессов распределения по продольному импульсу оказываются ф-циями только от безразмерного отношения
 (здесь
(здесь  ГэВ/с - проекция импульса вторичной частицы в системе центра инерции на ось соударения, a P- импульс налетающей частицы в той же системе) и не зависят явным образом от энергии [т. н. скейлинг Фейнмана (R. Feynman, 1969)]. Раннее эксперим. указание на такое поведение инклюзивных процессов было получено в космич. лучах и впервые надёжно установлено на ускорителе ИФВЭ (Серпухов, 1968). Скейлинг Фейнмана объясняется на основе партонной модели.
ГэВ/с - проекция импульса вторичной частицы в системе центра инерции на ось соударения, a P- импульс налетающей частицы в той же системе) и не зависят явным образом от энергии [т. н. скейлинг Фейнмана (R. Feynman, 1969)]. Раннее эксперим. указание на такое поведение инклюзивных процессов было получено в космич. лучах и впервые надёжно установлено на ускорителе ИФВЭ (Серпухов, 1968). Скейлинг Фейнмана объясняется на основе партонной модели.От энергии сталкивающихся частиц оказывается практически не зависящим также распределение по числу частиц, образующихся в множественном процессе. В этом случае вероятность рождения h частиц пропорциональна ф-ции лишь от отношения
 , где
, где 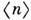 - ср. множественность при данной энергии.
- ср. множественность при данной энергии.Такое свойство подобия получило назв. скейлингa KNO [Кобы - Нильсена - Олесена (Z. Koba, H. В. Nielsen, P. Olesen), 1972]. В отличие от скейлин-гов Бьёркена и Фейнмана, наблюдающийся в опыте KNO-скейлинг не имеет общепризнанного теоретич. объяснения.
M. и. может быть использована для предсказания поведения формфакторов адронов при больших переданных импульсах и определения структурных функций (см. Кваркового счёта правила).
В связи с попытками объяснить в рамках квантовой теории поля (КТП) скейлинг Бьёркена с пач. 1970-х гг. обсуждалась возможность того, что Дайсона уравнения в КТП допускают масштабно-инвариантное решение. Для перенормируемой КТП этот вопрос оказывается связанным с поведением эффективного заряда при
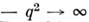 , к-рое определяется видом т. н. ф-ции Гелл-Мана - Лоу (см. Ренормализационная группа). Для M. и. необходимо, чтобы эта ф-ция обращалась в нуль при нек-ром значении эфф. заряда. В этом случае при достаточно больших значениях
, к-рое определяется видом т. н. ф-ции Гелл-Мана - Лоу (см. Ренормализационная группа). Для M. и. необходимо, чтобы эта ф-ция обращалась в нуль при нек-ром значении эфф. заряда. В этом случае при достаточно больших значениях  эфф. заряд совпадает с положением нуля и ур-ния ренормализац. группы для вершинных частей обладают масштабно-инвариантными решениями, вообще говоря, с нек-рой аномальной размерностью. Такая ситуация реализуется также в теории фазовых переходов2-го рода (с той, однако, разницей, что эта задача определена в трёхмерном пространстве, а не в четырёхмерном пространстве-времени и рассматривается ПК-, а не УФ-предел) [см. ниже].
эфф. заряд совпадает с положением нуля и ур-ния ренормализац. группы для вершинных частей обладают масштабно-инвариантными решениями, вообще говоря, с нек-рой аномальной размерностью. Такая ситуация реализуется также в теории фазовых переходов2-го рода (с той, однако, разницей, что эта задача определена в трёхмерном пространстве, а не в четырёхмерном пространстве-времени и рассматривается ПК-, а не УФ-предел) [см. ниже].Примеры M. и. с нетривиальными аномальными размерностями имеются в двумерном пространстве-времени (см. Двумерные модели КТП). Для неренормируемой КТП оказывается, что масштабно-инвариантные решения с необходимостью обладают инвариантностью относительно более общего конформного преобразования, что даёт возможность использовать для их нахождения методы конформной КТП (см. Конформная инвариантность в КТП).
В квантовой хромодинамике (КХД) асимптотическая свобода приводит к тому, что ф-ция Гелл-Мана - Лоу обращается в нуль при нулевом значении офф. заряда. В этом случае ур-ния ренормализац. группы дают для структурных ф-ций решение, к-рое является ф-цией не только от отношения
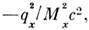 но также слабо (логарифмически) зависит непосредственно от
но также слабо (логарифмически) зависит непосредственно от  . Скейлинг Бьёркена справедлив в КХД с той точностью, с какой этой дополнит, зависимостью от -q2 можно пренебречь. Такое нарушение скейлинга Бьёркена должно наблюдаться в экспериментах по изучению неупругих процессов в достаточно широком диапазоне изменения - q2.
. Скейлинг Бьёркена справедлив в КХД с той точностью, с какой этой дополнит, зависимостью от -q2 можно пренебречь. Такое нарушение скейлинга Бьёркена должно наблюдаться в экспериментах по изучению неупругих процессов в достаточно широком диапазоне изменения - q2.Лит.: Боголюбов H. H., Ширков Д. В., Введение в теорию квантованных полей, 4 изд., M., 1984, гл. 9; Саrruthers P., Broken scale invariance in particle physics, "Phys. Repts", 1971, v. 1 G, p. 1; Hикитин Ю. П., Розенталь И. Л., Теория множественных процессов, M., 1976; Джекив P., Приближенная масштабная инвариантность, в кн.: Трейман С., Джекив Р., Гросс Д., Лекции по алгебре токов, пер. с англ., M., 1977, гл. 7. Ю. M. Макеепко.
Масштабная инвариантность в теории фазовых переходов 2-го рода. Эти переходы разбиваются на неск. классов эквивалентности, причём в рамках одного класса особенности термодинамич. величин в совершенно разл. системах описываются одними и теми же степенными законами. Так, напр., изотропные ферромагнетики, антиферромагнетики и сегнетоэлектрики попадают в один класс эквивалентности, а критические точки жидкость - пар, двухкомпонентные растворы, изин-говский ферромагнетик - в другой.
При фазовом переходе 2-го рода происходит спонтанное нарушение симметрии- в низкотемпературной фазе оказывается отличным от нуля т. н. параметр порядка (вектор намагниченности в ферромагнетиках, вектор поляризации в сегнетоэлектриках и т. п.). При темп-pax, близких к точке фазового перехода Т с, параметр порядка сильно флуктуирует, причём характерный размер флуктуации (корреляц. радиус
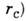 неограниченно растёт по мере приближения к Т с.
неограниченно растёт по мере приближения к Т с.С матем. точки зрения задача описания критич. флуктуации сводится к вычислению корреляционных функций типа
 - компонента параметра порядка,
- компонента параметра порядка, . В точке фазового перехода
. В точке фазового перехода  бесконечен, а следовательно, отсутствует естеств. единица длины. Подобное изменение всех расстояний (масштабное преобразование) в отсутствие характерного размера не может изменить состояния системы, т. к. это преобразование сводится к изменению единицы длины. При масштабном преобразовании сильно флуктуирующие величины преобразуются согласно закону
бесконечен, а следовательно, отсутствует естеств. единица длины. Подобное изменение всех расстояний (масштабное преобразование) в отсутствие характерного размера не может изменить состояния системы, т. к. это преобразование сводится к изменению единицы длины. При масштабном преобразовании сильно флуктуирующие величины преобразуются согласно закону 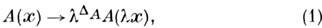
где
 - критический показатель оператора
- критический показатель оператора 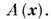
Существует бесконечный набор локальных неприводимых операторов
 к-рые получаются из
к-рые получаются из  , грубо говоря, "возведением в степень" и дифференцированием по координатам c и к-рые преобразуются при масштабном преобразовании в соответствии с законом (1). Критич. показатели
, грубо говоря, "возведением в степень" и дифференцированием по координатам c и к-рые преобразуются при масштабном преобразовании в соответствии с законом (1). Критич. показатели 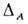 зависят от размерности пространства d, от числа компонент h параметра порядка, от конкретного вида оператора
зависят от размерности пространства d, от числа компонент h параметра порядка, от конкретного вида оператора  , но не зависят от структуры вещества на межатомных расстояниях.
, но не зависят от структуры вещества на межатомных расстояниях.Неизменность равновесного распределения критич. флуктуации при масштабном преобразовании приводит к след, тождествам Уорда для корреляц. ф-ций:
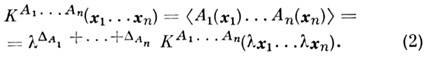
Для важного случая парных корреляц. ф-ций тождества (2) в сочетании с соображениями инвариантности относительно трансляций и вращений полностью определяют вид этих ф-ций:

где-
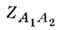 константы. Парные корреляц. ф-ции в нек-рых случаях можно измерить экспериментально; напр., эксперименты по рассеянию света в критич. точке жидкость - пар позволяют получить информацию о парной корреляц. ф-ции плотности вещества.
константы. Парные корреляц. ф-ции в нек-рых случаях можно измерить экспериментально; напр., эксперименты по рассеянию света в критич. точке жидкость - пар позволяют получить информацию о парной корреляц. ф-ции плотности вещества.Небольшое изменение темп-ры или включение слабого внеш. поля (магн. поля, давления и т. п.) выводит систему из точки фазового перехода. Корреляц. радиус становится конечным, хотя и превышает межатомное расстояние а. Зависимость r с от внеш. поля h и приведённой темп-ры
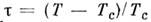 также определяется законами подобия. Если
также определяется законами подобия. Если 

где
 - критич. показатель оператора плотности энергии. Если
- критич. показатель оператора плотности энергии. Если 

Здесь
 - критич. показатель параметра порядка.
- критич. показатель параметра порядка.Ясно, что поведение парных корреляц. ф-ций для расстояний
 будет таким же, как и в точке фазового перехода, а при
будет таким же, как и в точке фазового перехода, а при  корреляц. ф-ции экспоненциально убывают. Поэтому для сингулярной части теплоёмкости С получаем оценку:
корреляц. ф-ции экспоненциально убывают. Поэтому для сингулярной части теплоёмкости С получаем оценку:
Восприимчивость системы c определяется корреляц. ф-цией параметра порядка:
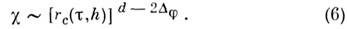
При
 появляется отличное от нуля среднее
появляется отличное от нуля среднее  , причём вблизи точки перехода
, причём вблизи точки перехода 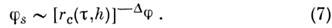
Ф-лы (3) - (7) показывают, что поведение сингулярной части теплоёмкости, восприимчивости и параметра порядка вблизи
 в случаях, когда либо
в случаях, когда либо  либо
либо  равны нулю, определяется двумя критич. индексами
равны нулю, определяется двумя критич. индексами 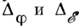 . Критич. индексы
. Критич. индексы  и т. п. приближённо вычислены методом эпсилон-разложения.
и т. п. приближённо вычислены методом эпсилон-разложения.Лит.: Паташинекий А. 3., Покровский В. Л., Флуктуационная теория фазовых переходов, 2 изд., M., 1982;
Вильсон К., Когут Д да., Ренормализационная группа и е-разложение, пер. с англ., M., 1975. С. Б. Хохлачёв.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
