КРИСТАЛЛОАКУСТИКА

КРИСТАЛЛОАКУСТИКА

       

изучает особенности распространения акустич. волн в кристаллах, а также влияние анизотропии физ. св-в кристаллов па хар-ки акустич. волн (особенности их поляризации, поглощения и отражения, дифракции и др.).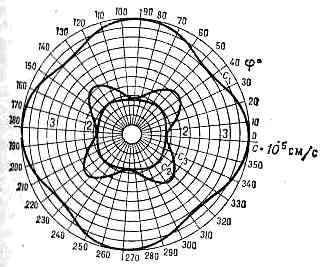

Анизотропия фазовых скоростей продольной с, и поперечных с2 и с3 упругих волн в плоскости (100) кристалла Bi12GeO20.

В кристаллах могут распространяться как объёмные, так и поверхностные акустические волны (ПАВ). Объёмные акустич. волны распространяются в кристалле так же, как в газах и жидкостях,— в любом направлении. ПАВ распространяются вдоль свободных поверхностей (границ) кристалла либо вдоль границ раздела двух кристаллов.

Анизотропия упругих св-в кристаллов существенно сказывается на хар-ре распространения акустич. волн. В кристалле, в отличие от изотропного тв. тела, в каждом направлении распространяются три упругие волны: продольная и две поперечных. Каждая из них имеет свою фазовую скорость, к-рая зависит от направления распространения волны в кристалле (рис.). В ряде направлений, соответствующих осям симметрии высокого порядка (см. СИММЕТРИЯ КРИСТАЛЛОВ), скорости двух поперечных волн могут совпадать. В таких направлениях, наз. акустическими осями кристалла, возможно распространение поперечных волн с произвольной поляризацией, как в изотропном теле. Суперпозиция линейно поляризованных волн позволяет получить эллиптич. и круговую поляризации сдвиговых волн. Анизотропия упругих св-в кристалла приводит к тому, что направление потока энергии акустич. волны Р не совпадает с направлением волн вектора k. Угол g между векторами Р и k может составлять десятки градусов. Вследствие этого даже при отсутствии дисперсии групповая скорость в кристаллах может не совпадать с фазовой. Характерно, что даже при распространении волн вдоль направлений высокого порядка симметрии поток энергии для сдвиговых волн может отклоняться от направления распространения волны, причём направление вектора потока энергии зависит от поляризации волны. В случае распространения сдвиговых волн вдоль акустич. осей это явление, по аналогии с оптикой, наз. внутренней конической рефракцией. Угол конич. рефракции в кварце, напр., составляет 17°, в LiNbO3 =8°, в NaCl=10°, в КСl=21°.

Анизотропия кристаллов усложняет также законы отражения и преломления акустич. волн на границах раздела сред: падающая волна при отражении и преломлении может расщепляться на неск. волн разных типов, в т. ч. и поверхностных. Пространственная дисперсия, обусловленная периодичностью крист. решётки, приводит к вращению плоскости поляризации сдвиговых волн (т. н. акустическая активность). Затухание звука в кристаллах определяется его рассеянием на микродефектах и дислокациях, поглощением вследствие вз-ствия упругой волны с тепловыми колебаниями крист. решётки — фононами, поглощением, обусловленным термоупругими и тепловыми эффектами. В металлах и ПП существует специфич. вид поглощения звука вследствие вз-ствия УЗ с эл-нами проводимости (см. АКУСТОЭЛЕКТРОННОЕ ВЗАИМОДЕЙСТВИЕ), а в ферромагнетиках и сегнетоэлектриках дополнит. поглощение связано с доменными процессами.

Нелинейная К. занимается исследованием вз-ствия акустич. волн в кристаллах: генерации акустич. гармоник и волн комбинац. частот, вз-ствий с электрич. полями и эл.-магн. волнами (см. НЕЛИНЕЙНОЕ ВЗАИМОДЕЙСТВИЕ АКУСТИЧЕСКИХ ВОЛН). Исследование нелинейного вз-ствия упругих волн в кристаллах имеет значение не только для объяснения поглощения звука, но также для описания тепловых фононных вз-ствий и лежит в основе теории работы нелинейных акустич. устройств — корреляторов, конволюторов. УЗ волны в кристаллах используются для создания ультразвуковых и гиперзвук. линий задержки, акустооптич. устройств и устройств акустоэлектроники.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

КРИСТАЛЛОАКУСТИКА

- раздел физ. акустики, в к-ром изучаются законы распространения акустич. волн в кристаллах и взаимодействия волн с разл. видами возбуждений в кристаллах (электронами, спинами, дефектами решётки и др.). В К. обычно используются волны УЗ- и гиперзвукового диапазонов. В кристалле скорость распространения упругих волн, их поляризация и поглощение зависят от направления распространения относительно кристаллографич. осей. Вследствие этого направление потока звуковой энергии в кристалле в общем случае не совпадает с нормалью к волновому фронту, т. е. перемещение фазы волны и её энергии происходит вдоль разл. направлений. Для многих кристаллов характерно существование выделенных направлений, вдоль к-рых преим. распространяется энергия звуковых колебаний. В анизотропной среде усложняются картина отражения и преломления звука, характер нелинейного взаимодействия УЗ-волн и др.

Описанные эффекты характерны и для поверхностных акустических волн, упругая анизотропия к-рых сказывается на их структуре: в зависимости от среза кристалла и от направления распространения поверхностной волны в плоскости этого среза изменяются характер движения частиц среды в волне вблизи границы кристалла (форма траекторий, их ориентация относительно поверхности кристалла) и глубина проникновения волны в глубь кристалла.

Особенностью распространения упругих волн в кристаллах является их взаимодействие с разл. подсистемами (макроскопическими электрич. и магн. полями, электронами, спинами и др.) кристаллов. Так, в кристаллах, обладающих пьезоэффектом, распространение акустич. волны сопровождается образованием переменного электрич. поля, движущегося вместе с волной деформации; в полупроводниках и металлах волна деформации вызывает движение и перераспределение свободных носителей (см. Акустоэлектронное взаимодействие);в магн. кристаллах упругая волна сопровождается волной переменного магн. поля, обусловленного магнитострикцией, и т. д. Для всех типов кристаллов характерно взаимодействие УЗ-волн с дефектами кристаллич. структуры, в первую очередь с дислокациями. Взаимодействие механич. деформаций с разл. подсистемами в значит, степени определяет поглощение УЗ, механизмы акустич. нелинейности, анизотропию скорости звука и даже обусловливает возникновение в кристаллах новых типов волн, как объёмных (связанные магнитоупругие волны в магн. кристаллах), так и поверхностных.

Распространение упругих воли в анизотропной среде. Эффекты упругой анизотропии в К. обычно описываются применительно к распространению в кристалле плоских волн. Фазовая скорость упругих волн определяется тензором модулей упругости 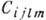, устанавливающим в линейном приближении связь между упругими напряжениями 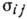и вызвавшими их деформациями : .

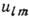Тензор 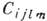симметричен относительно перестановки пар индексов ij и lт, а также относительно перестановки индексов внутри каждой нары. В общем случае он имеет 21 независимую компоненту, однако вследствие симметрии кристалла число независимых и неравных нулю компонент может быть меньше.

Направление распространения плоской волны задаётся волновой нормалью - единичным вектором п, параллельным волновому вектору k и нормальным волновому фронту. Компоненты вектора смещений и связаны между собой вытекающими из ур-ний движения упругой анизотропной среды ур-ниями Грина - Кристоффеля:

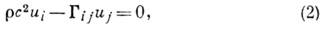
где 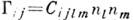- упругий тензор Грина - Кристоффеля, с( п) - фазовая скорость акустич. волны, распространяющейся в направлении п, 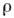- плотность кристалла. Фазовая скорость определяется из условия

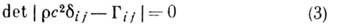
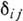( - символ Кронекера), а ур-ния (2) задают направление колебат. движения частиц среды в волне, т. е. поляризацию акустич. волны. В общем случае вдоль произвольного направления в кристалле могут распространяться 3 упругие волны с разл. фазовыми скоростями и со взаимно ортогональными векторами поляризации. В отличие от изотропной среды разделение акустич. волн на продольные и поперечные в кристаллах, в общем случае, невозможно, поскольку направления колебаний, как правило, не совпадают с направлением распространения и не ортогональны ему. Тем не менее принята следующая классификация упругих волн в кристаллах. Волна, вектор колебат. смещения к-рой составляет наим. угол с направлением распространения, наз. квази продольной QL. Две другие волны, направления колебаний в к-рых почти перпендикулярны направлению распространения, наз. квазипоперечными QT; последние часто классифицируют дополнительно по величине их фазовой скорости, выделяя быстрые FT и медленные ST квазипоперечные волны.

Особые направления в кристаллах. В кристаллах имеются особые направления - продольные и поперечные нормали и оси. Продольной нормалью наз. направление, вдоль к-рого распространяется чис-топродольная волна, а две другие волны обязательно поперечны. Поперечная нормаль представляет собой направление, вдоль к-рого распространяется лишь одна чистая волна - поперечная Т, поляризация двух других - QL и QT - геометрически ничем не выделена. Др. типом особых направлений являются акустич. оси - направления, для к-рых скорости обеих квазипоперечных волн совпадают. Вдоль акустич. оси в кристалле распространяется множество квазипоперечных волн, имеющих одну и ту же фазовую скорость, но различающихся векторами поляризации; их ориентация произвольна в плоскости, перпендикулярной вектору поляризации квазипродольной волны. Помимо линейно поляризованных волн вдоль акустич. осей могут распространяться также волны с более сложной поляризацией - циркулярно или эллиптически поляризованные волны, их вектор смещения в каждой точке пространства вращается в плоскости колебаний, описывая круг или эллипс. Наконец, если вдоль акустич. оси распространяются чистопро-дольная волна и множество чистопоперечных волн, то такое направление наз. продольной акустич. осью.

Все направления, связанные с элементами симметрии кристалла, являются особыми. Продольными нормалями являются оси симметрии и направления, перпендикулярные плоскостям симметрии. Для осей 3-го, 4-го и 6-го порядков скорости обеих поперечных волн совпадают, так что эти направления представляют собой продольные акустич. оси. Все направления, лежащие в плоскости симметрии, и направления в плоскостях, перпендикулярных осям симметрии чётных (2-го, 4-го или 6-го) порядков, являются поперечными нормалями, причём векторы колебаний чистопоперечных волн перпендикулярны плоскости распространения. Ориентация продольных и поперечных нормалей, а также акустич. осей может и не быть связанной с направлениями высокой симметрии. Так, напр., в триклинных кристаллах, где оси и плоскости симметрии отсутствуют, обязательно существуют продольные нормали и акустические оси.

Характеристические поверхности. Фазовые скорости упругих волн в кристаллах зависят от направления распространения. Наглядно такая зависимость представляется с помощью поверхности, образованной концами векторов фазовых скоростей для всевозможных направлений распространения. Поверхность фазовых скоростей состоит из трёх полостей, каждая из к-рых отвечает одному из типов упругих волн. Полость, отвечающая квазипродольным волнам, охватывает полости, соответствующие квазипоперечным волнам, не имея, как правило, с ними общих точек. Полости квазипоперечных волн пересекаются (или касаются) либо в отд. точках, либо вдоль линий; совокупность таких общих точек определяет направления акустич. осей в кристалле. Форма поверхности скоростей передаёт симметрию упругих свойств кристалла - наличие и положение осой и плоскостей симметрии. В изотропной среде поверхность скоростей превращается в две концентрич. сферы, причём две поверхности, отвечающие поперечным волнам разл. поляризации, сливаются в одну сферу. В кристаллах поверхности скоростей представляют собой сложные геом. образы, поэтому на практике используют сечения таких поверхностей плоскостями разл. ориентации, обычно связанными с элементами симметрии кристалла (рис. 1).

Чаще в К. используются две др. характеристич. поверхности: поверхность волновых векторов и поверхность медленностей (поверхность обратных скоростей или поверхность рефракции). Поверхность волновых векторов образуется концами векторов k==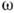n/с (n), проведённых из начала координат во всех направлениях и отвечающих одному и тому же значению круговой частоты 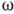. В пространстве волновых векторов эта поверхность описывается ур-нием 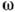(k)=const. Поверхность медленностей, образованная концами векторов п/с( п), отличается от поверхности волновых векторов лишь масштабным множителем 1/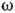. Поверхность волновых векторов, так же как и поверхность скоростей, состоит из трёх полостей, отвечающих упругим волнам разл. поляризации.

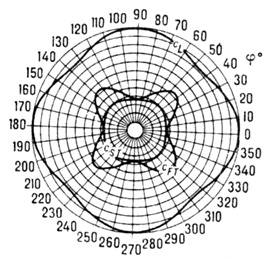
Рис. 1. Анизотропия фазовых скоростей продольной с _L и поперечных с _FT и c_ST упругих волн в плоскости (100) кристалла германата висмута.

Перенос акустической энергии в кристалле. При распространении плоской волны в анизотропной среде поток энергии отклоняется от волновой нормали. Скорость переноса энергии определяется вектором лучевой скорости с _q, равным отношению средней по времени плотности потока энергии I к средней плотности энергии W в волне: c_g=I/W. Понятие лучевой скорости играет ключевую роль в К., поскольку реально в среде распространяются не бесконечные волны, а пучки конечной апертуры, поэтому направления их распространения задаются переносом энергии, а не фазы (рис. 2). Лучевая скорость c_g совпадает с групповой скоростью 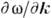, понятие к-рой вводится, когда акустич. пучок рассматривается как совокупность плоских волн, слегка отличающихся направлениями волновых нормалей. Компоненты вектора лучевой скорости упругой волны с волновой нормалью п и поляризацией V определяются соотношением

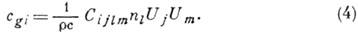
Проекция лучевой скорости c_g на направление волновой нормали п равна фазовой скорости волны с. Лучевая скорость равна фазовой только тогда, когда она направлена вдоль волновой нормали. Направления, для к-рых это имеет место, наз. направлениями чистых мод; вдоль них обычно направляют пучки УЗ-волн в акустоэлектронных и акустооптич. устройствах. Во всех остальных случаях лучевая скорость по абс. величине больше фазовой: с _q>c. Для мн. кристаллов угол 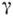между I и k; может достигать десятков градусов (напр., в кварце Si0₂, парателлурите ТеО ₂ и др.). Степень анизотропии лучевой скорости для упругих волн разл. поляризаций наглядно представляется с помощью поверхностей лучевых скоростей, образованных концами векторов c_g при всевозможных положениях луча в пространстве.

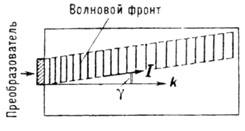
Рис. 2. Поток энергии I звуковой волны в анизотропном кристалле.

Лучевая скорость для волны с заданным вектором k направлена по нормали к поверхности волновых векторов 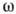(k)=const в точке, определяемой вектором k (рис. 3, а). Лучевая скорость совпадает с фазовой для тех точек этой поверхности, нормаль к к-рым направлена вдоль их радиусов-векторов (точки 1, 7 на рис. 3). Эти точки соответствуют экстремумам и др. стационарным точкам поверхности, в к-рых 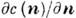= 0, и определяют направления чистых мод. Особый характер имеет зависимость с _q от направления п в тех кристаллах, у к-рых поверхность волновых векторов имеет не только выпуклые, но и вогнутые участки. При непрерывном перемещении направления волновой нормали с одного выпуклого участка на другой через область отрицат. кривизны вектор c_g дважды принимает одно и то же значение (точки 2, 6, рис. 3, б). Как отражение этого факта поверхность лучевых скоростей для соответствующего направления луча имеет самопересечение, образуя складку. Складки и др. топологич. особенности поверхности лучевых скоростей означают, что вдоль одного луча может распространяться несколько (в т. ч. и бесконечное множество) волн одной и той же частоты, принадлежащих к одной ветви колебаний, но различающихся направлениями своих волновых нормалей п: на рис. 3 ( б) вдоль луча Oz распространяются волны с волновыми нормалями, определяемыми точками 2, 4, 6 поверхности волновых векторов.

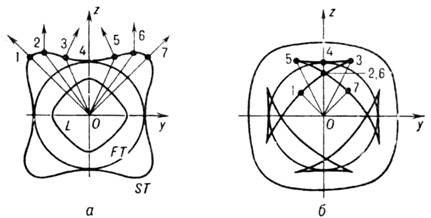
Рис. 3. Сечение поверхностей волновых векторов (а) и лучевых скоростей ( б) плоскостью (100). кристалла никеля. Стрелки на рис. а задают направления лучевых скоростей, отвечающих выделенным направлениям волновых нормалей.

Эффекты, связанные с топологией характеристич. поверхностей, особенно существенны при распространении излучения, создаваемого точечными источниками. В изотропной среде поток звуковой энергии, излучаемой точечным источнике равномерно распределён по всем направлениям. Если такой источник поместить в кристаллич. среду, то энергия излучения переносится преим. вдоль определ. кристаллографич. направлений. Этот эффект преимущественного распространения (концентрирования, каналирования) энергии акустич. излучения вдоль выделенных направлений в анизотропной среде наз. фононной фокусировкой. Анизотропия потока акустич. энергии от точечного источника характерна для всех кристаллов, однако фононная фокусировка возможна лишь в тех из них, поверхность волновых векторов (поверхность медленно-стей) к-рых содержит перегибы - области перехода от выпуклых участков поверхности к вогнутым, обладающие малой кривизной. Все волны с волновыми векторами k, лежащими в нек-рой окрестности точки перегиба (точки 3 или 5, рис. 3, а), переносят свою энергию в одном и том же направлении. Это направление соответствует точке возврата (лучи 3 или 5, рис. 3, б) на поверхности лучевых скоростей. Экспериментально явление фононной фокусировки наблюдалось при возбуждении акустич. ВЧ-волн (акустич. фононов) тепловым импульсом в нек-рых кристаллах (Ge, Si и др.) при низких темп-pax, когда возможно баллистич. (бесстолкновительное) распространение тепловых фононов по кристаллу. Измерение фононных потоков в кристаллах по разл. направлениям приводит к сложной картине углового распределения потока звуковой энергии, идущего от теплового источника (рис. 4).

Рис. 4. Фононная фокусировка в германии в направлении [100]. Светлые области соответствуют акустической энергии, приходящей от точечного источника на задней поверхности кристалла Ge.

Количественно эффект перераспределения потока энергии для луча q характеризуется коэф. концентрирования энергии А _q. Если вокруг q выделить конус лучей 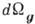, то все волновые нормали, к-рым соответствуют лучевые скорости внутри этого конуса, будут заключены внутри телесного угла 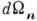, при этом А= 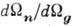. В изотропной среде А _q=1, в кристалле А _q может быть как больше, так и меньше единицы в зависимости от направления луча q. Для направлений, вдоль к-рых концентрируется поток энергии при фононной фокусировке, коэф. концентрирования обращается в бесконечность. Интенсивность излучения I в сферич. волне, излучаемой точечным источником в изотропной среде, убывает с расстоянием r как 1/r². 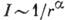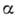В анизотропной среде зависимость I от расстояния различна для разных направлений; в направлениях концентрирования при фононной фокусировке I убывает с расстоянием гораздо медленнее, чем в изотропной среде: , где <2. В частности, может быть 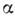=1, ³/₂, 4/3 и т. д. в зависимости от топологии поверхности волновых векторов.

При распространении упругих волн вдоль акустич. оси в кристалле может наблюдаться внутренняя коническая рефракция. При распространении поперечных волн разл. поляризации в направлении акустич. оси их лучевая скорость отклоняется от волновой нормали, причём направление отклонения зависит от поляризации волны. При повороте вектора смещения в плоскости поляризации соответствующий ему луч также поворачивается, описывая конус, являющийся геом. местом возможных направлений потока энергии. Внутр. конич. рефракция наблюдается, напр., при распространении чисто сдвиговых волн вдоль осей симметрии 3-го порядка (гл. оси симметрии [001] в тригональных кристаллах; направление [111] вдоль диагонали куба в кубич. кристаллах). Все возможные направления акустич. лучей в этом случае образуют круговой конус; отклонение лучей от акустич. оси характеризуется углом конич. рефракции, к-рый имеет во мн. кристаллах значит. величину и составляет, напр., в кальците СаСО ₃30°, в кварце 17°, в поваренной соли NaCl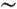10°, ниобате лития LiNbO₃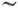8°.

В кристаллах (напр., в цинке в направлении [001]) возможно также явление внешней конической рефракции, к-рое состоит в том, что вдоль этого направления может распространяться множество квазипоперечных волн с волновыми нормалями, образующими конус вокруг направления луча. После прохождения границы раздела с изотропной средой такие волны преломляются и расходятся в изотропной среде по конич. поверхности (рис. 5).

Акустическая активность кристаллов. На гиперзвуковых частотах пространственная периодичность кристаллич. решётки приводит к пространственной дисперсии упругих свойств - становится существенной зависимость упругих напряжений не только от деформаций, но и от их пространственных производных. Поправки, связанные с пространственной дисперсией, пропорциональны отношению параметра решётки а к длине звуковой волны и всегда малы. Наличие же даже слабой пространственной дисперсии приводит к тому, что вдоль акустич. оси распространяется не множество поперечных волн с одной и той же фазовой скоростью с ₀, а две циркулярно поляризованные волны с векторами поляризации, вращающимися в противоположные стороны, и со слегка различающимися скоростями C₁ и с ₂: c_l,2=c₀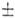kG/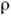, где k - волновое число, G - параметр акустич. гирации.

При возбуждении в направлении акустич. оси плоско поляризованной сдвиговой волны пространственная дисперсия приводит к явлению акустич. активности - способности кристалла поворачивать плоскость поляризации такой волны. Возбуждаемая волна является суперпозицией лево- и правополяризованной волн. По мере распространения в глубь кристалла увеличивается фазовый сдвиг между этими волнами из-за различия скоростей их распространения. Результирующее акустич. поле представляет собой плоскополяризованную волну, плоскость поляризации к-рой поворачивается по мере продвижения в глубь кристалла. Угол поворота 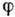линейно растёт с проходимым волной расстоянием L и пропорционален квадрату частоты: 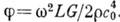По порядку величины 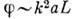и акустич. активность существенна только на гиперзвуковых частотах. Экспериментально акустич. активность наблюдалась в кварце: угол поворота на частоте 1 ГГц при длине пути 1 см составляет 130°. Искусств. акустич. активность возникает в магн. кристаллах типа иттриевого граната, помещённых в магн. поле, за счёт магнитоупругого взаимодействия (акустич. аналог Фарадея эффекта).

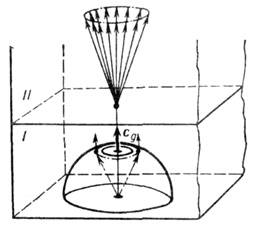
Рис. 5. Внешняя коническая рефракция на поверхности (001) кристалла Zn (I), граничащего с изотропной средой (II).

Особенности распространения упругих волн в пьезоэлектрических кристаллах. В кристаллах, обладающих пьезоэффектом, волна деформации сопровождается переменным электрич. полем, к-рое, в свою очередь, приводит к дополнит. механич. напряжениям, изменяющим деформацию в волне. В плоской волне напряжённость электрич. поля волны параллельна волновой нормали п и выражается через смещение и, а компоненты вектора смещения связаны между собой ур-ниями, совпадающими с ур-ниями (1) для непьезоэлектрич. среды, но с перенормированным за счёт пьезоэлектрич. взаимодействия тензором Кристоффеля-Грина:

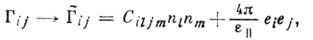
где 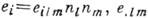- тензор пьезоэлектрич. постоянных, 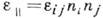- продольная диэлектрич. проницаемость. В целом для пьезоэлектрич. кристаллов картина распространения объёмных акустич. волн остаётся такой же, как и в непьезоэлектрических. Степень влияния пьезоэффекта на скорость распространения определяется квадратом константы электромеханич. связи К ²_U = 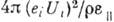, где U - поляризация волны. За счёт пьезоэффекта фазовая скорость с всегда больше величины скорости с ₀, определяемой только упругими модулями: с=с ₀ 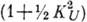. Разница между скоростями с и с ₀ наблюдается, напр., в пьезополупроводниках, где повышение концентрации свободных носителей позволяет исключить влияние пьезоэффекта: при больших концентрациях носители экранируют электрич. поле волны. Константа электромеханич. связи анизотропна, что увеличивает анизотропию акустич. свойств кристалла. В кристаллах имеются т. н. непьезоактивные направления, для к-рых константа электромеханич. связи равна нулю и влияние пьезоэффекта на распространение данной моды отсутствует.

Отражение и преломление акустических волн на границе раздела кристаллических сред. Анизотропия кристаллов усложняет характер отражения и преломления упругих волн на границе раздела сред. Направления волновых нормалей отражённой и преломлённой волн, как и в изотропном случае, определяются законами Снелля. Однако вследствие того что фазовая скорость зависит от направления волновой нормали, между углами падения, отражения и преломления нет простых соотношений (типа "угол падения равен углу отражения"), характерных для изотропной среды. При одном и том же угле падения углы отражения и преломления зависят от ориентации границы раздела относительно кристаллографич. осей. Направления лучей значительно отклоняются от направлений соответствующих нормалей, в результате акустич. энергия после отражения (или преломления) переносится в направлениях, существенно отличающихся от направлений, определяемых законами Снелля (подробнее см. Отражение звука).

Затухание акустических волн в кристалле. В кристаллах затухание акустич. волн обусловлено поглощением звука и рассеянием звука на микронеоднородностях. Для разл. групп кристаллов существуют специфич. механизмы поглощения, возникающие за счёт взаимодействия УЗ-волны с др. видами возбуждений в кристаллах. В полупроводниках и металлах важную роль играет поглощение, связанное с акустоэлектронным взаимодействием упругой волны со свободными носителями. В магн. кристаллах значит. вклад в поглощение УЗ вносит спин-фононное взаимодействие. В сегнетоэлектрич. кристаллах упругие волны взаимодействуют с НЧ-ветвью поперечных оптич. фононов (т. н. мягкой модой), что приводит к специфич. возрастанию УЗ-поглощения вблизи точки фазового перехода. В ферромагнетиках и сегнетоэлектриках возможно также дополнит. поглощение, обусловленное движением доменных стенок в УЗ-поле. Каждому из этих механизмов присуща своя зависимость коэф. поглощения от частоты УЗ-волны, направления её распространения и параметров кристалла.

Для большинства кристаллов характерно поглощение, обусловленное взаимодействием акустич. волны с дефектами кристаллов, в первую очередь - дислокац. поглощение. Под действием звуковой волны возникает колебат. движение сети дислокаций, петли к-рой закреплены в местах пересечения дислокаций и на точечных дефектах. Поглощение возникает за счёт диссипации энергии движущейся сети дислокаций (амплитуднонезависимое поглощение), за счёт отрыва петель дислокаций с мест их закрепления на точечных дефектах (амплитудно-зависимое поглощение) и, наконец, за счёт взаимодействия дислокаций непосредственно с кристаллич. решёткой, в результате чего появляются низкотемпературные пики поглощения - пики Бор-дони. Частотная зависимость для амплитудно-независимого поглощения носит резонансный характер, для поглощения вблизи пиков Бордони - релаксационный. Коэф. амплитудно-зависимого поглощения от частоты не зависит. Амплитудно-независимое поглощение характерно для гиперзвуковых частот и малых амплитуд колебаний; на более низких частотах и при достаточно больших звуковых интенсивпостях осн. роль играет амплитудно-зависимое поглощение.

Поглощение акустич. волн имеет место даже в совершенных кристаллах. Оно обусловлено взаимодействием упругой волны с тепловыми колебаниями решётки (т. н. решёточное, или фононное, поглощение). Для не слишком низких темп-р воздействие акустич. волны сводится к нарушению ею равновесного распределения фононов и к процессу релаксации в фононной системе (т. н. механизм Ахиезера). Макроскопически диссипация упругой энергии в рамках такого механизма описывается введением наряду с упругими напряжениями (1) вязких напряжений 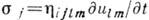, пропорциональных скорости деформации 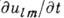, Коэф. пропорциональности 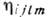составляет тензор решёточпых, или фононных, вязкостей. Коэф. решёточного поглощения 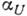квадратично зависит от частоты и пропорционален величин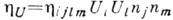е (где 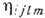- тензор вязкости):

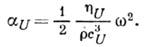
Анизотропия решёточного поглощения определяется структурой тензора вязкостей. Кроме того, в кристаллах, обладающих значит. теплопроводностью (напр., в металлах), важную роль играет поглощение, обусловленное теплообменом между разл. участками кристалла, по-разному нагретыми за счёт объёмных деформаций в звуковой волне (т. н. термоупругая диссипация). Термоупругая диссипация также приводит к квадратичной зависимости коэф. поглощения звука от частоты. При низких (гелиевых) темп-pax на высоких (гиперзвуковых) частотах осн. роль играет непосредственное нелинейное взаимодействие акустич. волны с тепловыми фононами - т. н. механизм Ландау-Румера (см. Фонон-фононное взаимодействие).

Поверхностные акустические волны в кристаллах. На свободной поверхности кристаллов распространяются поверхностные волны, являющиеся аналогами Рэлея волн в изотропном твёрдом теле. Волны рэлеев-ского типа в кристаллах образуются затухающими в глубь кристалла неоднородными волнами. Частицы среды в такой волне движутся по эллипсам, плоскость к-рых наклонена к поверхности кристалла под углом, зависящим от ориентации среза и направления распространения поверхностной волны в плоскости среза. Упругая анизотропия сказывается на характере распространения поверхностных волн точно так же, как и объёмных: возникает зависимость фазовой скорости от направления распространения и ориентации среза; поток энергии, оставаясь в плоскости распространения, отклоняется от направления волновой нормали; имеет место каналирование энергии поверхностных волн, излучаемых точечным источником, и т. д. Скорость поверхностной волны, как правило, меньше фазовой скорости любой из объёмных волн, распространяющихся в том же направлении. Однако в кристаллах со значит. степенью анизотропии (даже в кристаллах высокой симметрии - кубических и гексагональных) существуют срезы с особыми направлениями; по мере приближения направления распространения поверхностной волны к такому направлению возрастает глубина проникновения волны, скорость волны приближается к фазовой скорости VST медленной поперечной моды объёмных волн, и поверхностная волна превращается в линейно поляризованную объёмную волну (рис. 6). В то же время вдоль особого направления может распространяться чисто рэлеевская поверхностная волна со скоростью, большей 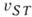. Эта волна даёт начало ветви псевдоповерхностных, или т. н. вытекающих, волн: при распространении вдоль направлений, отличных от особого, такие волны излучают в глубь кристалла объёмную волну. За счёт излучения псевдоповерхностные волны при распространении затухают. Помимо рэлеевских и псевдоповерхностных волн в ряде кристаллов распространяются поверхностные волны др. типов. В пьезо-электриках возможно распространение электроакус-тич. сдвиговых волн (волн Блюштейна - Гуляева), в магн. кристаллах существуют поверхностные магнитоупругие волны, в т. ч. чистосдвиговые.

Рис. 6. Скорости поверхностных волн при распространении их в плоскости (001) кристалла никеля: 1 - поверхностная волна рэлеевского типа, 2- псевдоповерхностная волна, FT и ST - скорости быстрых и медленных квазипоперечных волн.

Поверхностные акустич. волны в кристаллич. подложках нашли широкое применение в совр. технике в качестве линий задержек, фильтров, устройств обработки информации и др.

Нелинейные акустические эффекты в кристаллах. Нелинейная К. исследует распространение и взаимодействие УЗ-волн конечной амплитуды в кристаллах. В кристаллах имеет место решёточный ангармонизм (см. Колебания кристаллической решётки), описываемый соотношениями нелинейного Гука закона, но существуют и др. механизмы акустич. нелинейности. Они возникают за счёт взаимодействия упругих деформаций с разл. видами возбуждений кристалла. Так, в полупроводниках существенна электронная акустич. нелинейность, обусловленная нелинейной зависимостью концентрации носителей заряда от деформации, вызванной акустич. волной, в пьезоэлектрич. кристаллах значит. роль играют нелинейный пьезоэффект, электрострикция и т. <н.

В кристаллах наблюдаются те же нелинейные эффекты, что и в изотропных телах: генерация гармоник, нелинейное поглощение, нелинейное взаимодействие волн с образованием волн суммарной и разностной частоты, в т. ч. комбинац. рассеяние звука на звуке, и т. д. Однако нелинейная акустика кристаллов отличается сложностью и многообразием этих эффектов. Существование трёх ветвей акустич. колебаний увеличивает в кристаллах число видов нелинейного взаимодействия акустич. волн, разрешённых условиями фазового синхронизма. Возможность того или иного вида взаимодействия, а также его эффективность зависят от ориентации волновых нормалей взаимодействующих волн относительно кристаллографич. осей. Эффективность волнового взаимодействия в кристаллах связана со взаимным расположением взаимодействующих акустич. пучков. Она максимальна, когда совпадают направления лучей для всех волн, участвующих во взаимодействии. В кристаллах, однако, из-за различия фазовых и лучевых скоростей направления взаимодействующих пучков часто не совпадают даже при коллинеарности волновых векторов взаимодействующих волн.

Акустич. волны в кристаллах используют для создания УЗ- и гиперзвуковых линий задержки, резонаторов, разл. устройств акустоэлектроники и акустооптики, для излучения и приёма УЗ-сигналов, измерений механич. деформаций и напряжений, измерений модулей упругости и др. физ. величин.

Лит.: Федоров Ф. И., Теория упругих волн в кристаллах, М., 1965; Musgrave M. J. P., Crystal acoustics. Introduction to the study of elastic waves and vibrations in crystals, S. F., 1970; Труэлл Р., Эльбаум Ч., Чик Б., Ультразвуковые методы в физике твёрдого тела, пер. с англ., М., 1972; Фарнелл Дж., Свойства упругих поверхностных волн, в кн.: Физическая акустика, под ред. У. Мэзона и Р. Терстона, пер. с англ., т. 6, М., 1973; Auld В. A., Acoustic fields and waves in solids, v. 1-2, N. Y. , 1973; Александров К. С., Акустическая кристаллография, в кн.: Проблемы современной кристаллографии, М., 1975; Сиротин Ю. И., Шаскольская М. П., Основы кристаллофизики, 2 изд., М., 1979; Балакирев М. К., Гилинекий И. А., Волны в пьезокристаллах, Новосиб., 1982; Акустические кристаллы, под ред. М. П. Шаскольской, М., 1982; Вольф Д ж., Баллистические тепловые импульсы в кристаллах, в кн.: Физика за рубежом, пер. с англ., М., 1982; Лямов В. Е., Поляризационные эффекты и анизотропия взаимодействия акустических волн в кристаллах, М., 1983; Красильников В. А., Крылов В. В., Введение в физическую акустику, М., 1984. В. М. Левин, Л. А. Чернозатонский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.