- КИНЕТИКА ФИЗИЧЕСКАЯ
- КИНЕТИКА ФИЗИЧЕСКАЯ
-
микроскопич. теория процессов в статистически неравновесных системах. Она изучает методами квант. или классич. статистической физики процессы переноса энергии, импульса и в-ва в разл. физ. системах (газах, плазме, жидкостях, тв. телах), а также влияние на эти системы внеш. полей.В отличие от термодинамики неравновесных процессов и электродинамики сплошных сред, К. ф. исходит из представления о мол. строении рассматриваемых сред и силах вз-ствия между их ч-цами, что позволяет вычислить кинетические коэффициенты, диэлектрич. и магн. проницаемости и др. подобные хар-ки сплошных сред.К. ф. включает кинетическую теорию газов из нейтр. атомов или молекул, статистич. теорию неравновесных процессов в плазме, теорию явлений переноса в тв. телах (диэлектриках, металлах и ПП), кинетику магн. процессов и теорию кинетич. явлений, связанных с прохождением быстрых ч-ц через в-во. К ней же относится теория процессов переноса в квантовых жидкостях и кинетика фазовых переходов.В К. ф. используют существ. различие времён релаксации в неравновесных процессах. Напр., для газа из ч-ц или квазичастиц время свободного пробега между столкновениями значительно больше времени столкновения Dt. На временных интервалах, значительно превышающих Dt, в системе происходит усреднение хаотич. движений ч-ц («хаотизация», или «перемешивание», газа). Это даёт возможность перейти от описания неравновесного состояния ф-цией распределения ч-ц по всем координатам q и импульсам р к упрощённому описанию на основе одночастичной ф-ции распределения одной ч-цы по её координатам и импульсам (в этом случае можно считать, что все ч-цы ведут себя одинаково).Осн. метод К. ф.— построение и решение кинетического уравнения Больцмана для ф-ции распределения молекул f(q, p, t) в их фазовом пространстве (q, p). Произведение fdqdp есть ср. вероятное число молекул в элементе фазового объёма dqdp(dq= dx dy dz, dp=dpxdpydpz). Любой рассматриваемый неравновесный процесс связан с перераспределением молекул (атомов) в элементах фазового объёма за счёт их свободного движения или в результате столкновений. Ф-ция распределения f удовлетворяет кинетич. ур-нию Больцмана, учитывающему все возможные причины перераспределения молекул:df/dt+v•gradf+pдf/дp=Stf,где v — скорость молекул; v•gradf — изменение числа молекул в элементе фазового объёма, связанное с их движением; р•(дf/дp) — изменение числа молекул, вызванное действием внеш. сил; Stf — интеграл столкновений, определяющий разность числа молекул, приходящих в элемент объёма и убывающих из него вследствие столкновений.Для газа из одноатомных молекул или более сложных молекул, но без учёта их внутр. степеней свободыStf=?w(f'f'1-ff1)dp1dp'dp'1,где w — вероятность столкновения, связанная с дифференциальным эфф.сечением ds=(w/(v-v1))dp'dp'1, p, р1— импульсы молекул до столкновения, р', p'1 — их импульсы после столкновения, f, f1 — ф-ции распределения молекул до столкновения, f', f'1 — их ф-ции распределения после столкновения. В простейшем приближении Stf=-(f-f0)/t, где f0 — равновесная ф-ция распределения, t — ср. время релаксации.Для газа из сложных молекул, обладающих внутр. степенями свободы, напр. двухатомных молекул с собств. моментом вращения М, ф-ция распределения зависит также от М и нужно учесть увеличение фазового объёма молекулы, связанное с её вращением.К. ф. позволяет получить ур-ния баланса ср. плотностей массы, импульса и энергии. Напр., для газа плотность r, гидродинамич. скорость v и ср. энергия ? удовлетворяют ур-ниям баланса: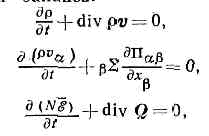 где Пab=?mvavbfdp — тензор плотности потока импульса, Q= ??vfdp — плотность потока энергии, N — число ч-ц.Если состояние газа мало отличается от равновесного, то в малых элементах объёма устанавливается локально-равновесное распределение, характеризуемое Максвелла распределением с темп-рой, плотностью и гидродинамич. скоростью, соответствующими рассматриваемому элементу объёма. В этом случае неравновесная ф-ция распределения мало отличается от локально-равновесной и решение кинетич. ур-ния даёт малую к ней поправку, пропорц. градиентам темп-ры grad Т и гидродинамич. скорости gradv. Неравновесный поток импульса даёт сдвиговую вязкость, а для газов с внутр. степенями свободы он содержит ещё член, пропорц. div v, к-рый приводит к объёмной вязкости. Плотность потока энергии Q пропорц. grad Т (обычная теплопроводность), а в случае смеси газов выражение для Q содержит ещё член, пропорц. градиенту концентрации gradс (Дюфура эффект). Поток в-ва в смеси газов содержит член, пропорц. градиенту концентрации (обычная диффузия), и член, пропорц. градиенту темп-ры (термодиффузия). Подобные соотношения наз. линейными соотношениями между термодинамич. силами и потоками. Для входящих в них коэфф. (напр., сдвиговой вязкости и объёмной вязкости, коэфф. теплопроводности, диффузии, термодиффузии, эффекта Дюфура) К. ф. даёт выражения через эфф. сечения столкновений, следовательно через константы межмол. вз-ствия. Кинетич. коэфф. для перекрёстных явлений, напр. для термодиффузии и для эффекта Дюфура, оказываются равными (частный случай общих соотношений взаимности Онсагера; (см. ОНСАГЕРА ТЕОРЕМА)).Ур-ния баланса импульса, энергии, числа ч-ц определ. сорта вместе с линейными соотношениями между термодинамич. силами и потоками позволяют получить Навье — Стокса уравнения, теплопроводности уравнение, ур-ние диффузии. Такой гидродинамич. подход к решению задач о переносе физ. величин справедлив, если длина свободного пробега l значительно меньше характерных размеров областей неоднородности.К. ф. позволяет исследовать явления переноса в разреженных газах и в том случае, когда отношение длины свободного пробега l к характерным размерам L системы (т. е. число Кнудсена l/L) уже не очень мало и имеет смысл рассматривать поправки порядка l/L (слабо разреженные газы). В этом случае ур-ния К. ф. позволяют объяснить явление температурного скачка на границе потока газа и тв. поверхности, а также скольжение потока в слое порядка l вблизи поверхности.Для сильно разреженных газов, когда l/L->1, гидродинамич. ур-ния неприменимы и необходимо решать кинетич. ур-ние с определёнными граничными условиями на поверхностях. Эти условия определяются ф-цией распределения молекул, рассеянных из-за вз-ствия со стенкой. Рассеянный поток может приходить в тепловое равновесие со стенкой (полная аккомодация), но в реальных случаях это не достигается. Для сильно разреженных газов роль коэфф. теплопроводности играют коэфф. теплопередачи. Напр., кол-во теплоты q, переносимое через ед. площади параллельных пластинок, между к-рыми находится разреженный газ, равно: q=c(T2- T1)/L, где T1 и T2 — темп-ры пластинок, L — расстояние между ними, c — коэфф. теплопередачи.Для описания процессов в плазме К. ф. пользуется двумя ф-циями распределения — эл-нов fe и ионов fi, удовлетворяющих системе двух кинетич. ур-ний. На ч-цы плазмы действуют силыF=Ze(E+1/c(vB)),где Ze — заряд ч-цы, Е — напряжённость электрич. поля, В— индукция магн. поля, удовлетворяющие Максвелла уравнениям. В ур-ния Максвелла входят ср. значения плотностей токов и зарядов. Их определяют при помощи ф-ций распределения fe и fi. Т. о., кинетич. ур-ния и ур-ния Максвелла представляют собой связанные системы ур-ний, описывающие все явления в плазме.К. ф. неравновесных процессов в диэлектриках основана на решении кинетич. ур-ния Больцмана для фононов крист. решётки (ур-ние Пайерлса). В частности, кинетич. ур-ние для фононов позволяет исследовать теплопроводность и поглощение звука в диэлектриках.К. <ф. металлов основана на решении кинетич. ур-ния для эл-нов с учётом их вз-ствия с фононами. Рассеяние эл-нов на фононах обусловливает появление электрич. сопротивления. К. ф. теоретически объясняет гальваномагнитные, термоэлектрич. и термомагн. явления, скин-эффект и циклотронный резонанс в ВЧ полях и ряд др. эффектов в металлах. Для сверхпроводников она объясняет особенности их ВЧ поведения.К. ф. магнитных явлений основана на решении кинетич. ур-ния для магнонов, что позволяет вычислить магн. восприимчивость систем в перем. полях, изучить кинетику процессов намагничивания.К. ф. неравновесных процессов в жидкостях требует более общего подхода, т. к. в этом случае одно-частичная ф-ция распределения не раскрывает специфики явлений и необходимо рассматривать двухчастичную ф-цию распределения. Однако для жидкости возможен гидродинамич. подход, т. к. для неё существуют медленно меняющиеся гидродинамич. переменные — плотность числа ч-ц, плотность энергии, плотность импульса. В течение малого времени релаксации в макроскопически малых объёмах жидкости устанавливается локально-равновесное распределение, подобное равновесному распределению Гиббса, но с темп-рой, хим. потенциалом и гидродинамич. скоростью, к-рые соответствуют рассматриваемому малому объёму жидкости. Для достаточно медленных процессов и когда масштабы пространств. неоднородности значительно меньше масштаба корреляции между ч-цами жидкости, неравновесная ф-ция распределения близка к локально-равновесной и можно найти к ней поправку, пропорц. градиентам темп-ры, гидродинамич. скорости и хим. потенциалам компонентов. Полученная равновесная ф-ция распределения позволяет вычислить потоки импульса, энергии и в-ва и вывести ур-ния Навье — Стокса, теплопроводности и диффузии. Кинетич. коэфф. оказываются в этом случае пропорц. пространственно-временным корреляц. ф-циям потоков энергии, импульса и в-ва данного сорта (ф-лы Грина— Кубо).
где Пab=?mvavbfdp — тензор плотности потока импульса, Q= ??vfdp — плотность потока энергии, N — число ч-ц.Если состояние газа мало отличается от равновесного, то в малых элементах объёма устанавливается локально-равновесное распределение, характеризуемое Максвелла распределением с темп-рой, плотностью и гидродинамич. скоростью, соответствующими рассматриваемому элементу объёма. В этом случае неравновесная ф-ция распределения мало отличается от локально-равновесной и решение кинетич. ур-ния даёт малую к ней поправку, пропорц. градиентам темп-ры grad Т и гидродинамич. скорости gradv. Неравновесный поток импульса даёт сдвиговую вязкость, а для газов с внутр. степенями свободы он содержит ещё член, пропорц. div v, к-рый приводит к объёмной вязкости. Плотность потока энергии Q пропорц. grad Т (обычная теплопроводность), а в случае смеси газов выражение для Q содержит ещё член, пропорц. градиенту концентрации gradс (Дюфура эффект). Поток в-ва в смеси газов содержит член, пропорц. градиенту концентрации (обычная диффузия), и член, пропорц. градиенту темп-ры (термодиффузия). Подобные соотношения наз. линейными соотношениями между термодинамич. силами и потоками. Для входящих в них коэфф. (напр., сдвиговой вязкости и объёмной вязкости, коэфф. теплопроводности, диффузии, термодиффузии, эффекта Дюфура) К. ф. даёт выражения через эфф. сечения столкновений, следовательно через константы межмол. вз-ствия. Кинетич. коэфф. для перекрёстных явлений, напр. для термодиффузии и для эффекта Дюфура, оказываются равными (частный случай общих соотношений взаимности Онсагера; (см. ОНСАГЕРА ТЕОРЕМА)).Ур-ния баланса импульса, энергии, числа ч-ц определ. сорта вместе с линейными соотношениями между термодинамич. силами и потоками позволяют получить Навье — Стокса уравнения, теплопроводности уравнение, ур-ние диффузии. Такой гидродинамич. подход к решению задач о переносе физ. величин справедлив, если длина свободного пробега l значительно меньше характерных размеров областей неоднородности.К. ф. позволяет исследовать явления переноса в разреженных газах и в том случае, когда отношение длины свободного пробега l к характерным размерам L системы (т. е. число Кнудсена l/L) уже не очень мало и имеет смысл рассматривать поправки порядка l/L (слабо разреженные газы). В этом случае ур-ния К. ф. позволяют объяснить явление температурного скачка на границе потока газа и тв. поверхности, а также скольжение потока в слое порядка l вблизи поверхности.Для сильно разреженных газов, когда l/L->1, гидродинамич. ур-ния неприменимы и необходимо решать кинетич. ур-ние с определёнными граничными условиями на поверхностях. Эти условия определяются ф-цией распределения молекул, рассеянных из-за вз-ствия со стенкой. Рассеянный поток может приходить в тепловое равновесие со стенкой (полная аккомодация), но в реальных случаях это не достигается. Для сильно разреженных газов роль коэфф. теплопроводности играют коэфф. теплопередачи. Напр., кол-во теплоты q, переносимое через ед. площади параллельных пластинок, между к-рыми находится разреженный газ, равно: q=c(T2- T1)/L, где T1 и T2 — темп-ры пластинок, L — расстояние между ними, c — коэфф. теплопередачи.Для описания процессов в плазме К. ф. пользуется двумя ф-циями распределения — эл-нов fe и ионов fi, удовлетворяющих системе двух кинетич. ур-ний. На ч-цы плазмы действуют силыF=Ze(E+1/c(vB)),где Ze — заряд ч-цы, Е — напряжённость электрич. поля, В— индукция магн. поля, удовлетворяющие Максвелла уравнениям. В ур-ния Максвелла входят ср. значения плотностей токов и зарядов. Их определяют при помощи ф-ций распределения fe и fi. Т. о., кинетич. ур-ния и ур-ния Максвелла представляют собой связанные системы ур-ний, описывающие все явления в плазме.К. ф. неравновесных процессов в диэлектриках основана на решении кинетич. ур-ния Больцмана для фононов крист. решётки (ур-ние Пайерлса). В частности, кинетич. ур-ние для фононов позволяет исследовать теплопроводность и поглощение звука в диэлектриках.К. <ф. металлов основана на решении кинетич. ур-ния для эл-нов с учётом их вз-ствия с фононами. Рассеяние эл-нов на фононах обусловливает появление электрич. сопротивления. К. ф. теоретически объясняет гальваномагнитные, термоэлектрич. и термомагн. явления, скин-эффект и циклотронный резонанс в ВЧ полях и ряд др. эффектов в металлах. Для сверхпроводников она объясняет особенности их ВЧ поведения.К. ф. магнитных явлений основана на решении кинетич. ур-ния для магнонов, что позволяет вычислить магн. восприимчивость систем в перем. полях, изучить кинетику процессов намагничивания.К. ф. неравновесных процессов в жидкостях требует более общего подхода, т. к. в этом случае одно-частичная ф-ция распределения не раскрывает специфики явлений и необходимо рассматривать двухчастичную ф-цию распределения. Однако для жидкости возможен гидродинамич. подход, т. к. для неё существуют медленно меняющиеся гидродинамич. переменные — плотность числа ч-ц, плотность энергии, плотность импульса. В течение малого времени релаксации в макроскопически малых объёмах жидкости устанавливается локально-равновесное распределение, подобное равновесному распределению Гиббса, но с темп-рой, хим. потенциалом и гидродинамич. скоростью, к-рые соответствуют рассматриваемому малому объёму жидкости. Для достаточно медленных процессов и когда масштабы пространств. неоднородности значительно меньше масштаба корреляции между ч-цами жидкости, неравновесная ф-ция распределения близка к локально-равновесной и можно найти к ней поправку, пропорц. градиентам темп-ры, гидродинамич. скорости и хим. потенциалам компонентов. Полученная равновесная ф-ция распределения позволяет вычислить потоки импульса, энергии и в-ва и вывести ур-ния Навье — Стокса, теплопроводности и диффузии. Кинетич. коэфф. оказываются в этом случае пропорц. пространственно-временным корреляц. ф-циям потоков энергии, импульса и в-ва данного сорта (ф-лы Грина— Кубо).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
.
