НОРМАЛЬНЫЕ ВОЛНЫ

НОРМАЛЬНЫЕ ВОЛНЫ

       

(собственные волны), бегущие гармонические волны в линейной динамич. системе с пост. параметрами, в к-рой можно пренебречь поглощением и рассеянием энергии. Н. в. явл. обобщением понятия нормальных колебаний на открытые области пр-ва и незамкнутые волноводные системы, в т. ч. на однородные и неоднородные безграничные среды, разл. типы волноводов и волн. каналов, струны, стержни, замедляющие системы, цепочки связанных осцилляторов (напр., LC-цепочки).

Совокупность Н. в. данной системы обладает след. св-вами. 1) Каждая Н. в. явл. свободным (без стороннего воздействия) движением системы и может быть возбуждена независимо от других Н. в. спец. выбором нач. условий. 2) Произвольный волн. процесс в системе без источников можно однозначно представить в виде суперпозиции Н. в. 3) Спектр частот Н. в. явл. сплошным, реальные процессы могут быть представлены в виде интегральных сумм Н. в. 4) В случае монохроматпч. процессов средний по периоду поток энергий равен сумме потоков энергии отдельных Н. в.

Понятие Н. в. применяется и к системам конечной протяжённости, где, однако, их следует рассматривать как вынужденные движения, возбуждаемые гармонич. источниками, распределёнными вне области наблюдения, а совокупность Н. в. должна быть дополнена спадающими от источников «ближними» полями.

В наиб. простом случае сред и волноводных систем, параметры к-рых не меняются вдоль нек-рого направления (напр., вдоль оси z), H. в. синусоидальны не только во времени, но и в пространстве и обладают неизменной поперечной структурой:

ai=Ai(r1, w) cos(wt-kzz),

где w — циклич. частота, kz — продольное волн. число (с ним связаны продольная длина волны lz=2p/k2 и фазовая скорость vф=w/kz), AI — распределение амплитуды одного из компонентов волн. поля, зависящее только от поперечных к оси z координат r1. Связь между w и kz определяет дисперсионные св-ва Н. в. (см. ДИСПЕРСИЯ ВОЛН) и, как правило, явл. неоднозначной — одному значению kz соответствует набор Н. в. с разными частотами. Н. в., частоты и волн. числа к-рых принадлежат отдельной непрерывной дисперсионной ветви многозначной функции w=w(kz), относятся к одной норм. моде системы (или просто моде). Моды различаются либо амплитудными и поляризац. структурами полей, либо физ. природой процессов.

В однородных безграничных средах Н. в. принято называть однородные плоские волны, распространяющиеся в произвольных направлениях. В изотропных средах волн. число k0 не зависит от направления распространения, а поляризация поперечных волн может быть произвольной. В анизотропных и гиротропных средах k0 зависит от направления распространения (соответственно различают обыкновенные и необыкновенные Н. в.). На рис. 1 приведены дисперсионные ветви Н. в. в изотропной неизотермич. плазме. Частотные спектры поперечных эл.-магн. и ленгмюровских волн ограничены снизу электронной плазменной частотой wре, спектр ионнозвуковых волн ограничен сверху ионной плазменной частотой wpi; значения частот и волн. чисел, ограничивающих дисперсионную ветвь, наз. к р и т и ч е с к и м и для данной моды.

В экранированных волноводных системах (металлич. радиоволноводы, волноводы акустические, упругие пластины, звук. каналы в водоёмах с тв. дном и т. д.) существует дискретное множество мод, поля к-рых локализованы в поперечных сечениях отражающими границами (экранами).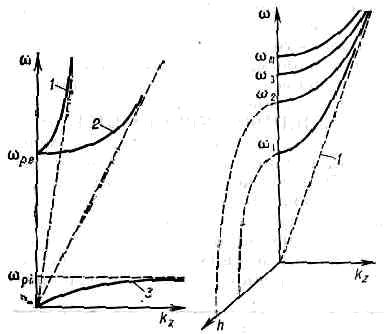

Рис. 1. Дисперсия норм. волн в изотропной плазме: .1 — ветвь поперечных электромагнитных, 2 —ленгмюровских, 3 — ионно-звуковых волн.

Рис. 2. Дисперсия норм. волн в экраниров. системах: 1 — ветвь квазистатич. мод; h — декремент экспоненциально спадающих мод.

Структура мод определяется формой поперечных двухмерных норм. колебаний (kz=0, д/дz=0), а критич. частоты — собств. частотами этих колебаний wn, где n=1, 2, ... (рис. 2). При w

В открытых волн. каналах поперечная локализация Н. в. основана на эффекте полного внутр. отражения либо на резких границах раздела сред (диэлектрич. волноводы, световоды), либо на плавных неоднородностях среды (звук. каналы в океане и атмосфере, ионосферные радиоканалы, каналы внутр. волн в океане и т. д.). Предельным случаем волн. каналов явл. поверхности раздела сред, вдоль к-рых могут распространяться поверхностные Н. в.

Значение Н. в. определяется их структурной устойчивостью по отношению к малым, а также к медленным и плавным изменениям параметров системы, что допускает широкое (хотя и не вполне строгое) обобщение понятия Н. в. на системы со слабыми потерями и нелинейными вз-ствиями. Метод Н. в, (т. е. разложение полей по Н. в.) применяется при изучении природных волн. явлений (эл.-магн., акустич., гидродинамических и т. д.) и при конструировании волн. технич. устройств.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

НОРМАЛЬНЫЕ ВОЛНЫ

(собственные волны)- бегущие гармонич. волны в линейной динамической системе с пост. <параметрами, в к-рой можно пренебречь поглощением и рассеянием энергии. <Н. в. являются обобщением понятия нормальных колебаний на открытыеобласти пространства и незамкнутые волноводные системы, в т. ч. на однородныеи неоднородные безграничные среды, разл. типы волноводов и волновых каналов, <струны, стержни, замедляющие системы, цепочки связанных осцилляторов идр.
Совокупность Н. в. обладает след. свойствами.1. Каждая Н. в. является свободным (без стороннего воздействия) движениемсистемы и может быть возбуждена независимо от других Н. в. спец. выборомнач. условий. 2. Произвольный волновой процесс в системе без источниковможет быть однозначно представлен в виде суперпозиции Н. в. 3. Спектр частотН. в. является сплошным, реальные процессы могут быть представлены в видеинтегральных сумм Н. в.
Понятие Н. в. применяется и к системамконечной протяжённости, где, однако, их следует рассматривать как вынужденныедвижения, возбуждаемые гармонич. источниками, распределёнными вне областинаблюдения, а совокупность Н. в. должна быть дополнена спадающими от источников"ближними" долями. В объёмных резонаторах в диапазоне высоких собств. <частот допустимо описание процессов в виде суперпозиций как нормальныхколебаний с дискретным спектром, так и Н. в. со сплошным спектром. Такойдуализм динамич. поведения свойствен физ. объектам, включая природные каналы внутреннихволн, волн цунами в океане, сейсмич. волн в земной коре, радиоканалЗемля - ионосфера и др.
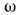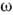В напб. простом случае сред и волноводиыхсистем, параметры к-рых не меняются вдоль нек-рого направления (напр.,вдоль оси z), H. в. синусоидальны не только во времени, но и в пространствеи обладают неизменной поперечной структурой: a_i= A_i(r₁,)cos(t - k_zz), где 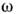- циклич. частота, k_z - продольное волновое число (сним связаны продольная длина волны 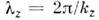и фазовая скорость 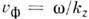),A_i- амплитудное распределение одной из компонент волнового поля, зависящеетолько от поперечных к оси z координат r.
Связь между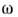 и k_z определяетдисперсионные свойства Н. в. и, как правило, является неоднозначной - одномузначению k_z соответствует набор Н. в. с разными частотами. <Н. в., частоты и волновые числа к-рых принадлежат отд. непрерывной дисперсионнойветви многозначной ф-ции 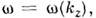относятся к одной нормальной моде системы (или просто моде). Моды различаютсялибо амплитудными и поляризац. структурами полей, либо фпз. природой процессов. <В случаях вырождения одной дисперсионной ветви соответствует неск. линейнонезависимых мод, их число наз. кратностью вырождения. Возможны также вырожденияН. в. при фиксир. значениях 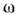и k_z,соответствующих точкам пересечения или касания дисперсионных ветвей.
Одно из наиб. важных свойств разложенийполей по Н. в. заключается в распространении принципа суперпозиции на нек-рыеэпергетич. характеристики движения. Так, в произвольном гармонич. процессе(представляющем сложную картину пространств. биений Н. в. с одинаковымичастотами, но разными длинами волн) полный поток энергии (усреднённый попериоду Т =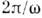 )равенсумме парциальных потоков энергии отд. Н. в. Волновые пакеты при своёмраспространении разбиваются на пакеты, объединяющие Н. в. одной моды; приэтом полная энергия процесса равна сумме энергий одномодовых пакетов. Понятиегрупповой скорости 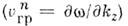может быть введено только для одномодовых волновых пакетов.
В однородных безграничных средах Н. в. <принято наз. однородные плоские волны, распространяющиеся в произвольныхнаправлениях. В изотропных средах волновое число k₀ независит от направления распространения, а поляризация поперечных волн можетбыть произвольной (двукратное поляризац. вырождение). В анизотропных игиротропных средах k₀ зависит от направления распространенпя, <а поляризац. вырождение снимается (соответственно различают обыкновенныеи необыкновенные Н. в.). На рис. 1 приведены дисперсионные ветви Н. в. <в изотропной неизотермич. плазме. Частотные спектры поперечных эл.-магн. <и ленгмюровских волн ограничены снизу электронной плазм, частотой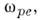 спектр понно-звуковых волн ограничен сверху ионной плазм. частотой 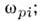значениячастот и волновых чисел, ограничивающих дисперсионную ветвь, наз. критическимидля данной моды.
В экранир. волноводных системах (металлич. <радиоволноводы, акустич. трубы, упругие пластины, звуковые каналы в водоёмахс твёрдым дном и т. д.) существует бесконечное счётное множество мод, поляк-рых локализованы в поперечных сечениях отражающими границами (экранами).Структура мод определяется формой поперечных двумерных нормальных колебаний(k_z=0, d/dz= 0), а критич. частоты мод - собств. частотами этихколебаний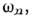 .=1, 2, ... (рис. 2). При 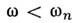данной моде соответствуют экспоненциально спадающие или нарастающие поля 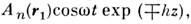каждое из к-рых, взятое в отдельности, не может переносить энергию. Однакокомбинации сдвинутых по фазе спадающих и растущих полей определяют "просачивание"энергии через закрптич. область, где волны распространяться не могут, -т. н. туннельный эффект.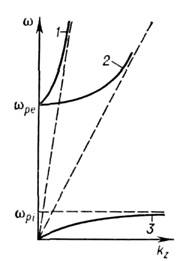

Рис. 1.Дисперсия нормальных волнв изотропной неизотермической плазме : 1 - поперечные электромагнитныеволны; 2 - ленгмюровские волны; 3 - ионно-звуковые волны.

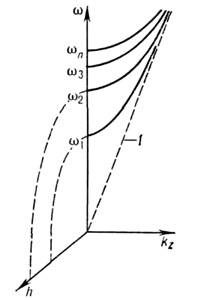
Рис. 2. Дисперсия нормальных волн в экранированныхсистемах: 1 - квазистатические моды; h - декремент экспоненциальноспадающих мод.

В волноводах с однородным заполнением фазовые 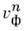и групповые 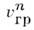скорости Н. в. и однородных плоских волн в среде заполнения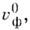 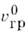связаны универсальным соотношением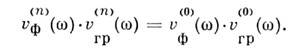

В коротковолновом пределе диапазона (k_z- >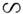) дисперсионныеветви мод стремятся к общей асимптоте (асимптотич. вырождение), совпадающейс ветвью однородных волн в среде заполнения (пунктирная линия 1 нарис. 2) . В акустич. трубах и неодносвязных радиоволноводах (в коаксиальныхи многожильных кабелях, а также в открытых длинных линиях) эта асимптотасама является одной из ветвей Н. в. системы - т. н. квазистатич. Н. в.,существующих при 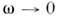и при любой частоте имеющих статич. поперечную структуру (напр., электростатическуюи магнитостатическую). В N- жильном кабеле квазистатич. моды N -кратновырождены, что используется в системах многоканальной передачи информации.
В открытых волновых каналах поперечнаялокализация Н. в. происходит в результате полного внутреннего отражения либона резких границах раздела сред (диэлектрич. волноводы, световоды), либона плавных неоднородностях среды (звуковые каналы в океане и атмосфере, <ионосферные радиоканалы, каналы внутр. волн в океане и др.). Совокупностьлокализованных (или захваченных) мод дискретна, но (в отличие от экранир. <систем) не является полной. В волновых каналах существует сплошное множествот. н. незахваченных мод, не спадающих при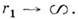
Предельным случаем волновых каналов являютсярезкие границы раздела сред, вдоль к-рых могут распространяться поверхностныеН. в.
Понятие Н. в. обобщается на продольно-периодич. <структуры: гофриров. волноводы, замедляющие системы, цепочки четырёхполюсников, <среды с равномерным шпром анизотропии (напр., жидкие кристаллы) и т. д.
Значение Н. в. в физике, технике, природеопределяется их уникальной структурной устойчивостью по отношению к малым, <а также к медленным и плавным изменениям параметров системы. Это свойстводопускает возможность довольно широкого (хотя и не вполне строгого) распространенияпонятия Н. в. на системы со слабыми потерями и нелинейными взаимодействиями, <искривлённые, деформированные, заполненные неоднородной средой, на системыс флуктуациями параметров и шероховатостями экранов. Метод Н. в. (т. е. <разложение полей по Н. в. модельных систем) применяется при изучении природныхволновых явлений (эл.-магн., акустич., гидродинамич., сейсмич., плазм.,гравитационных и т. д.) и при конструировании волноводных техн. устройств.

Лит.: Горелик Г. С., Колебания иволны, 2 изд., М., 1959; Вайнштейн Л. А., Электромагнитные волны, 2 изд.,М., 1988; Бреховских Л. <М., Волны в слоистых средах, 2 изд., М., 1973; ЗавадскийВ. Ю., Вычисление волновых полей в открытых областях и волноводах, М.,1972; Никольский В. В., Никольская Т. И., Электродинамика и распространениерадиоволн, 3 изд., М., 1989.

М. А. Миллер, Г. В. Пермитин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.