ВЕРБАЛЬНАЯ ПОДГРУППА

- подгруппа 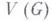группы G, порожденная всевозможными значениями всех слов из нек-рого множества когда независимо друг от друга пробегают всю группу G. В. п. нормальна; конгруэнция, определяемая с помощью В. п. на группе, является вербальной конгруэнцией (см. также Алгебраических систем многообразие).

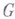Примеры В. п.: 1) коммутант группы , определяемый коммутатором 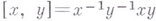; 2) n-й коммутант ; 3) члены нижнего центрального ряда

где 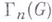- В. п., определяемая коммутатором

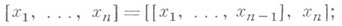
4) степень 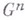группы , определяемая словом .

При любом гомоморфизме 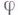справедливо равенство. . В частности, - вполне характеристическая подгруппа в G. Обратное верно для свободных групп, но не в общем случае: пересечение двух В. п. может п не быть В. п. Для прямого произведения групп

что, однако, уже неверно при переходе к декартову произведению.

Особо важную роль играют В. п. свободной группы Xсчетного ранга. Они составляют (дедекиндову) подре-шетку решетки всех ее подгрупп. В. п. обладает свойством "монотонности": если и , где ( означает, что является нормальным делителем группы X), то и .В частности, влечет .

Лит.:[1] Курош А. Г., Теория групп, 3 изд., М., 1967; [2] Нейман X., Многообразия групп, пер. с англ., М., 1969. О. Н. Головин.