ВЕДДЕРБЕРНА - МАЛЬЦЕВА ТЕОРЕМА

пусть А - конечномерная ассоциативная алгебра над полем Fс радикалом N и пусть факторалгебра A/N - сепарабельная алгебра (для алгебр над полем характеристики 0 это всегда выполнено); тогда алгебра Аразлагается (как линейное пространство) в прямую сумму радикала N и нек-рой полупростой подалгебры S

причем, если имеется другое разложение , где - полупростая подалгебра, то существует автоморфизм алгебры 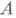, отображающий 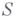на 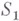(автоморфизм 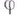является внутренним, т. е. существуют элементы 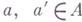такие, что 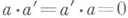и 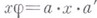для всех 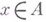, где 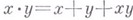). Существование указанного разложения получено Дж. Веддерберном [1], а единственность (с точностью до автоморфизма) полупростого слагаемого доказана А. И. Мальцевым [2]. Эта теорема вместе с теоремой Веддерберна (см. Ассоциативные кольца и алгебры )о строении полупростых алгебр составляет центральную часть классич. теории конечномерных алгебр.

Лит.:[1] Weddеrburn J. Н. М., "Ргос. London Math. Soc.", ser. 2, 1908, v. 6, p. 77-118; [2] Мальцев А. И., "Докл. АН СССР", 1042, т. 36, № 1, с. 42-5; [3] Albert A. A., Structure of algebras, N. Y., 1939; [4] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969. Л. А. Бокуть.