ВАРИАЦИЯ ФУНКЦИОНАЛА

первая вариация - обобщение понятия дифференциала функции одного переменного, главная линейная часть приращения функционала вдоль определенного направления; используется в теории экстремальных задач для получения необходимых и достаточных условий экстремума. Именно такой смысл вкладывается в термин "В. ф.", начиная с работы Ж. Лагранжа [1] (1760). Ж. Лагранж рассматривал по преимуществу функционалы классического вариационного исчисления вида:

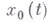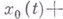
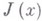Если заданную функцию заменить на и подставить в выражение для , то при допущении о непрерывной дифференцируемости интегранта L имеет место следующее равенство:

где при . Функцию 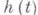часто наз. в а-риацией функции и иногда обозначают через . Выражение , представляющее собой функционал относительно вариаций h, наз. первой вариацией функционала и обозначают через . В применении к функционалу (1) выражение для первой вариации имеет вид:

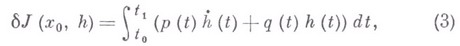
где

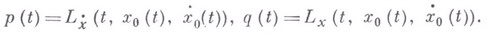
Равенство нулю первой вариации для всех hявляется необходимым условием экстремума функционала Для функционала (1) из этого необходимого условия и основной леммы вариационного исчисления (см. Дюбуа-Реймона лемма).следует уравнение Эйлера:

Путем, аналогичным (2), определяются и вариации более высоких порядков (см., напр., в ст. Вторая вариация функционала).

Общее определение первой вариации в бесконечномерном анализе было дано Р. Гато (R. Gateaux) в 1913 (см. Гато вариация). По сути своей определение Гато тождественно с определением Лагранжа. Первая вариация функционала является однородным, но не обязательно линейным функционалом, В. ф. при дополнительном предположении о линейности и непрерывности (по /г) выражения наз. обычно Гато производной. Термины "вариация Гато", "производная Гато", "дифференциал Гато" более употребимы, чем В. ф.; термин "В. ф." сохранился лишь для функционалов классического вариационного исчисления (см. [3]).

Лит.- [1] La grange J., Essai d'une nouvelle methode pour determiner les maxima et les minima des formules mteg-rales mdefimes, Turin, 1762; [2] Gateaux R., "Bull. Soc. Math. France", 1919, T. 47. с. 70-96; [3] Лаврентьев М. А., Люстерник Л. А., Курс вариационного исчисления, 2 изд., М -Л.. 1950. В. М. Тихомиров.