ЧЕБЫШЕВСКИЙ ЦЕНТР

ограниченного множества Миз метрич. пространства - элемент для к-рого

Величина (*) есть чебышевский радиус множества М. Если линейное нормированное пространство является сопряженным к нек-рому линейному нормированному пространству, то любое ограниченное множество имеет хотя бы один Ч. ц. Существует банахово пространство и трехточечное множество в нем, не имеющее Ч. ц. Для того чтобы каждое ограниченное множество банахова пространства Xимело не более одного Ч. ц., необходимо и достаточно, чтобы Xбыло равномерно выпуклым по каждому направлению, т. е. чтобы для любого и любого существовало такое число что если и то 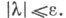Ч. ц. каждого ограниченного множества Миз линейного нормированного пространства Xразмерности большей двух принадлежит выпуклой оболочке этого множества тогда и только тогда, когда Xгильбертово. Ч. ц.- частный случай более общего понятия наилучшей N-сети.

Лит.:[1] Итоги науки. Математический анализ. 1967, М., 1969, с. 75 - 132.
Ю. Н. Субботин.