ЧЕБЫШЕВА МНОГОЧЛЕНЫ

первого рода - многочлены, ортогональные на отрезке [-1, 1] с весовой функцией

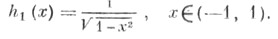
Для стандартизованных Ч. м. справедливы формула

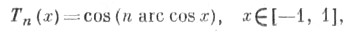
и рекуррентное соотношение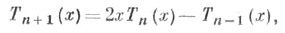

с помощью к-рых находят последовательно

T₀ (x) = 1, T₁(x) = x, Т₂ (х)=2х ^2-1,

T₃(x) = 4x³ - З х, T₄(x) = 8x⁴ - 8x² + 1,

Т ₅ (х)= 16x⁵ - 20x³ + 5 х, ....
Ортонормированные Ч. м.: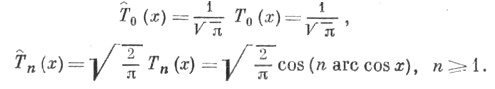

Старший коэффициент многочлена Т _n (х) при равен 2ⁿ-1. Поэтому Ч. п. с единичным старшим коэффициентом определяются формулой

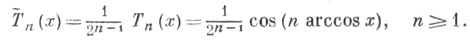
Нули многочлена Т _п(x), определяемые равенством

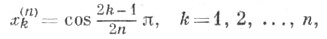
часто применяются в качество узлов интерполяционных и квадратурных формул. Многочлен Т _п (х)является решением дифференциального уравнения

Многочлен 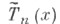наименее отклоняется от нуля на отрезке [-1, 1], т. е. для всякого другого многочлена 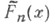степени пс единичным старшим коэффициентом выполняется условие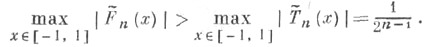

С другой стороны, для всякого многочлена Q_n(x) степени не выше и, удовлетворяющего условию

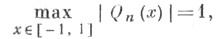при любом 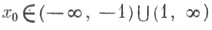имеет место неравенство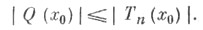
Если функция f(x)непрерывна на отрезке [-1, 1] и ее модуль непрерывности удовлетворяет условию Дини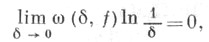

то эта функция разлагается в ряд Фурье - Чебышева 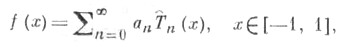сходящийся равномерно на отрезке [-1, 1]. Коэффициенты этого ряда определяются по формуле

Если же функция f(х)непрерывно дифференцируема рраз на отрезке [-1, 1], причем ее р-я производная f ^(Р) (х) удовлетворяет условию Липшица порядка т. е. то имеет место неравенство

где постоянная с ₁ не зависит от пи х.
Ч. м. второго рода определяются равенством

Эти многочлены ортогональны на отрезке [-1, 1] с весовой функцией

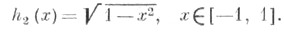
Для всякого многочлена с единичным старшим коэффициентом справедливо неравенство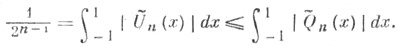

Ч. м. были введены в 1854 П. Л. Чебышевым (см. [1]).
Обе системы Ч. м. являются частными случаями ультрасферических многочленов и Якоба многочленов.

Лит.:[1] Чебышев П. Л., Полн. собр. соч., т. 2, М.- Л., 1947, с. 23-51; [2] Сегё Г., Ортогональные многочлены, пер. с англ., М., 1962.
П. К. Суетин.