ЧАПЛЫГИНА ТЕОРЕМА

ЧАПЛЫГИНА ТЕОРЕМА

о дифференциальном неравенстве: если в дифференциальном неравенстве


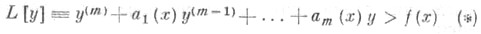
все ai и f суммируемы на [x0, х 1],то существует такое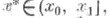 не зависящее от f, что y(х) > z(x),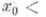 где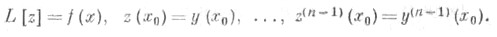

При этом

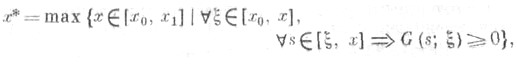
где 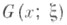- соответствующая функция Коши, т. e. решение уравнения L[G]=0, 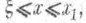удовлетворяющееначальным условиям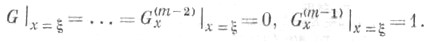


Таким образом, при т=1, а также для неравенства y"-y>f(x)получается x*=x1, тогда как для неравенства у"+у>f (х)получают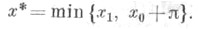


Аналогичные утверждения справедливы: для нестрогих неравенств; для сравнения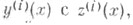 i=l,......,m-1; для начальных условий вида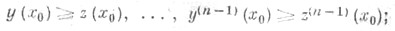


для решения неравенства (*) при х<х0.
Теорема была получена С. А. Чаплыгиным в 1919.

Лит.:[1 ] Мамедоd Я. Д., Аширов С., Атдаев С., Теоремы о неравенствах, Аш., 1980.
См. также лит. при статье Дифференциальное неравенство.
А. Д. Мышкис.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Смотреть что такое "ЧАПЛЫГИНА ТЕОРЕМА" в других словарях:

  • ЧАПЛЫГИНА МЕТОД — метод приближенного решения задачи Коши для системы обыкновенных дифференциальных уравнений 1 го порядка, состоящий в одновременном построении двух семейств последовательных приближении к ее решению. Напр., в случае задачи Коши для одного… …   Математическая энциклопедия

  • Теорема Жуковского — Теорема Жуковского  теорема о подъёмной силе тела, обтекаемого плоскопараллельным потоком идеальной жидкости или газа. Сформулирована Н. Е. Жуковским в 1904 году. Формулировка теоремы: Подъёмная сила крыла бесконечного размаха… …   Википедия

  • Чаплыгина неравенство —         одно из важнейших дифференциальных неравенств. Если y’ (x) = f (x, y) и функции u (х) и v (x) удовлетворяют дифференциальным неравенствам u’ (х) f (x, u) > 0 и v’ (x) f (x, v) < 0 (x0 ≤ x ≤ x1) и u (х0) = v (x0) = y0, то решение y (x)… …   Большая советская энциклопедия

  • ЖУКОВСКОГО ТЕОРЕМА — теорема о подъёмной силе, действующей на тело, находящееся в плоскопараллельном потоке жидкости или газа. Сформулирована Н. Е. Жуковским в 1904. Согласно этой теореме, подъёмная сила обусловлена связанными с обтекаемым телом вихрями (т. н.… …   Физическая энциклопедия

  • СРАВНЕНИЯ ТЕОРЕМА — в теории дифференциальных уравнений теорема, утверждающая наличие определенного свойства решений дифференциального уравнения (или системы дифференциальных уравнений) в предположении, что нек рым свойством обладает вспомогательное уравнение или… …   Математическая энциклопедия

  • Жуковского теорема — Теорема Жуковского  теорема о подъёмной силе тела, обтекаемого плоскопараллельным потоком идеальной жидкости или газа. Сформулирована Н. Е. Жуковским в 1904 году. Формулировка теоремы: Подъемная сила крыла бесконечного размаха равна произведению… …   Википедия

  • Жуковского теорема — устанавливает связь между вектором аэродинамической силы, приложенной к профилю, и циркуляцией скорости Γ вокруг него и формулируется так: при безотрывном обтекании произвольного профиля однородным установившимся потенциальным потоком идеальной… …   Энциклопедия техники

  • Жуковского теорема — Схемы обтекания задних кромок профиля. Жуковского теорема устанавливает связь между вектором аэродинамической силы, приложенной к профилю, и циркуляцией скорости Γ вокруг него и формулируется так: при безотрывном обтекании произвольного профиля… …   Энциклопедия «Авиация»

  • Жуковского теорема — Схемы обтекания задних кромок профиля. Жуковского теорема устанавливает связь между вектором аэродинамической силы, приложенной к профилю, и циркуляцией скорости Γ вокруг него и формулируется так: при безотрывном обтекании произвольного профиля… …   Энциклопедия «Авиация»

  • Франкль, Феликс Исидорович — Феликс Исидорович Франкль Felix Frankl …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»