ХАРАКТЕРИСТИКА

- одно из основных понятий в теории дифференциальных уравнений с частными производными. Роль X. проявляется в существенных свойствах этих уравнений, таких, как локальные свойства решений, разрешимость различных задач, их корректность и др.
Пусть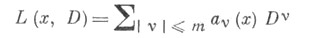

- линейный дифференциальный оператор с частными производными порядка m, a

- его символ. Здесь -мультииндекс, | v |=v₁+ .. .+v_n,

Пусть S -гиперповерхность, определенная в уравнением причем при

В этом случае Sназ. характеристической поверхностью, или характеристикой, для оператора L( х, D). Другие названия X.: характеристическое многообразие, характеристическая линия (в случае
Ниже рассмотрен пример задачи Коши. Пусть S - произвольная (не обязательно характеристическая) гиперповерхность в определенная уравнениями

Пусть u₀, ..., u_m-1 -функции, определенные на Sв окрестности Uточки 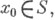и поставлена задача Коши

относительно неизвестной функции и. Здесь f-заданная функция, L(x, D) - заданный линейный дифференциальный оператор порядка т, п - ортонормированный вектор к S. Считая, для определенности, заменой переменных
приходят к уравнению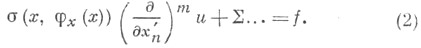

Невыписанное выражение под знаком не содержит частных производных от функции ипо порядка т. Возникают два случая:

В первом случае деление уравнения (2) на приводит к уравнению, разрешенному относительно старшей частной производной по переменной т. е. записанному в нормальной форме. Начальным условиям можно придать вид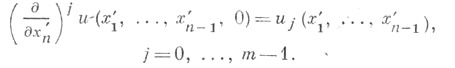

Такая постановка задачи Коши хорошо изучена и, напр. при аналитически заданных функциях в уравнении и в начальных условиях, существует единственное решение этой задачи в классе аналитич. ций в достаточно малой окрестности точки х ₀. Во втором случае точка х ₀ является характеристической, а если равенство (1) верно для всех то поверхность Sявляется X. В этом случае начальные данные не могут быть произвольными и исследование задачи Коши усложняется.
Напр., для уравнения

могут быть заданы начальные условия на одной из его X. x₁=0:

Если функция u₁ отлична от постоянной, то задача Коши (3), (4) не имеет решения в пространстве С ². Если же функция u₁ постоянна, напр. равна то решение неединственно в С ², т. к. им может быть любая функция вида

u(x₁, х₂) = ах₁ + b (х ₁) + и₀ (х ₂). где
Таким образом, задача Коши существенно различается в зависимости от того, заданы ли начальные данные на характеристической поверхности или нет.
X. обладает свойством инвариантности при преобразовании независимых переменных: если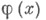 есть решение уравнения (1) и если преобразование переводит удовлетворяет уравнению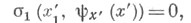

где

Другое свойство X. таково, что относительно X. Sоператор L(x, D )является внутренним дифференциальным оператором.
Эллиптические линейные дифференциальные операторы определяются как операторы, для к-рых не существует X. (действительных). Определение гиперболич. и параболич. операторов также тесно связано с понятием X. Так, линейный дифференциальный оператор 2-го порядка относится к гиперболич. типу, если он имеет два семейства X., и к параболическому, если - одно. Знание X. дифференциального уравнения позволяет свести это уравнение к более простому виду. Напр., пусть задано гиперболич. уравнение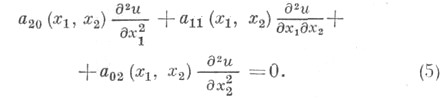

Для него уравнение X. (1) имеет вид

Последнее уравнение определяет два различных семейства X.:

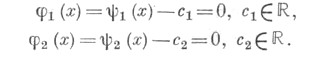
Существуют две X. из этих семейств такие, что соответствующие им функции и определяют замену переменных по формулам

и приводят уравнение (5) к канонич. виду

Для нелинейного дифференциального уравнения

где -мультииндексы, причем X. Sопределяется как гиперповерхность в 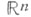с уравнением 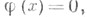причем пр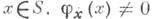и и 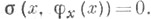Символ в атом случае для оператора (6), задаваемого функцией F( х, и, v, w), определяется так:

Кроме переменных хи очевидно,может зависеть от Пусть, напр., задано уравнение 1-го порядка (m = 1). Кроме того, для простоты п=2. Уравнение (6) принимает вид

с функцией F(x, у, z, p, q). Уравнение X.:

Т. к. решение этого уравнения 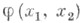фактически может зависеть от и, 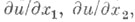то ее задают в параметрич. виде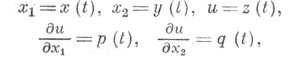

причем эти функции удовлетворяют обыкновенным дифференциальным уравнениям

x'(t) = F_p, y'(t) = F_q, z'(t) = pF_p + qF_q, _P'(t)=-F_x-pF_z, g'(t)=-F_y-qF_z.

Геометрически это определяет т. н. характеристическую полосу (при Проекция этой полосы на пространство (x(t), y(t), z(t))определяет такую кривую линию в что в каждой своей точке она касается плоскости с направляющими коэффициентами p(t), q(t). Эта кривая также наз. X. уравнения (6).

Лит.:[1] Мизохата С., Теория уравнений с частными производными, пер. с япон., М., 1977: [2] Камке Э., Справочник по дифференциальным уравнениям в частных производных первого порядка, пер. с нем., М., 1966; [3] Хартман Ф., Обыкновенные дифференциальные уравнении, пер. с англ., М., 1970; [4] Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; [5] К ошляков Н. С., Глинер Э. Б., Смирнов М. М., Уравнения в частных производных математической физики, М., 1970: [6] Владимиров В. С., Уравнения математической физики, 4 изд., М., 1981; [7] Михлин С. Г., Курс математической физики, М., 1968; [8] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 5 изд., М., 1977.
Ю. В. Комленко.