ХАРАКТЕР

группы - гомоморфизм данной группы в нек-рую стандартную абелеву группу А. Обычно в качестве . берется либо мультипликативная группа k* нек-рого поля k, либо подгруппа

группы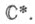 Понятие X. группы было первоначально введено для конечных групп Gи А=Т (впрочем, в этом случае всякий X. принимает значения в Т).
Изучение X. групп сводится к случаю абелевых групп, поскольку имеется естественный изоморфизм между группами Hom (G,А) и Hom (G/(G, G), A), где (G, G) - коммутант группы G. Характеры составляют линейно независимую систему в пространстве всех k-значных функций на G. Характер однозначно продолжается до X. групповой алгебры k[G]. Характеры являются одномерными линейными представлениями группы G над k;понятие характера представления группы в одномерном случае совпадает с понятием X. группы. Иногда X. группы называют X. любого ее конечномерного представления (и даже само это представление).
Характер топологической группы G- это непрерывный гомоморфизм Если G - локально компактная абелева группа, то ее X. разделяют точки, т. е. для любых а, существует такой X. что 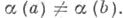Для хаусдорфовых абелевых групп G это утверждение, вообще говоря, неверно (см. [3]). Характер алгебраической группы G над алгебраически замкнутым полем К - это рациональный гомоморфизм
В теории чисел важную роль играют X. мультипликативной группы кольца вычетов по модулю k, к-рые взаимно однозначно соответствуют Дирихле характерам (mod k):характеру отвечает характер Дирихле определяемый формулой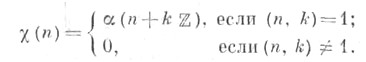

См. также Характеров группа.

Лит.:[1] Борель А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Моррис С., Двойственность Понтрягнна и строение локально компактных абелевых групп, пер. с англ., М., 1980: [3] Xьюитт Э., Рoсс К., Абстрактный гармонический анализ, пер. с англ., т. 1, М., 1976.
А. Л. Онищик.