УРАВНЕНИЕ

- аналитическая запись задачи о разыскании значений аргументов, при к-рых значения двух данных функций равны. Аргументы, от к-рых зависят эти функции, наз. обычно неизвестными, а значения неизвестных, при к-рых значения функций равны,- решениями, или корнями, У.; о таких значениях неизвестных говорят, что они удовлетворяют данному У.
Совокупность решений данного У. зависит от области Мзначений, допускаемых для неизвестных. У. может не иметь решений в М, тогда оно наз. неразрешимым в области М. Если У. разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Напр., У. х ⁴-4 = 0 неразрешимо в области рациональных чисел, но имеет два решения: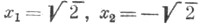 в области действительных чисел и четыре решения: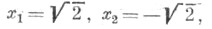 - в области комплексных чисел.
У. sin x = 0 имеет бесконечное множество решений: в области действительных чисел.
Если У. имеет решениями все числа области М, то оно наз. тождеством в области М.
Совокупность У., для к-рых требуется найти значения неизвестных, удовлетворяющие одновременно всем этим У., наз. системой У.; совокупность значений неизвестных, удовлетворяющих одновременно всем У. системы, наз. решением системы. Две системы У. (или два У.) наз. равносильными, если каждое решение одной системы (одного У.) является решением другой системы (другого У.), и наоборот, причем обе системы (оба У.) рассматриваются в одной и той же области.
Процесс разыскания решений У. заключается обычно н замене У. равносильным. В нек-рых случаях приходится заменять данное У. другим, для к-poro совокупность корней шире, чем у данного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних корней, то все полученные корни преобразованного У. проверяют подстановкой в исходное У.
Наиболее полно изучены алгебраические уравнения;их решение было одной из важнейших задач алгебры в 16-17 вв. Если f(x) - трансцендентная функция, то У. f(x)=0 наз. трансцендентным, причем в зависимости от вида f(x)оно наз. тригонометрическим У., логарифмическим У., показательным У.
При практич. решении У. обычно применяются различные приближенные методы (см., напр., Линейная алгебра;численные методы).
Среди систем У. простейшими являются системы линейных уравнений. Решение системы У. (не обязательно линейных) сводится, вообще говоря, к решению одного У. при помощи т. н. исключения неизвестных (см. Исключения теория).
В теории чисел рассматриваются т. н. неопределенные У., изучение решений к-рых составляет предмет теории диофантовых уравнений.
В общем случае У. является записью задачи о разыскании таких элементов анек-рого множества А, что F(а)=Ф(а), где Fи Ф - заданные отображения множества Аво множество В. Если Аи В - множества чисел, то возникают У. рассмотренного выше вида. Если Аи В - множества точек в многомерных пространствах, то получаются системы У. Если Аи В- множества функций, то в зависимости от характера отображения могут получаться дифференциальные уравнения обыкновенные, дифференциальные уравнения с частными производными, интегральные уравнения и др. виды У.
По материалам одноименной статьи из БСЭ-3.