- УНИПОТЕНТНАЯ МАТРИЦА
квадратная матрица Анад кольцом, для к-рой матрица А -Е п, где п - порядок матрицы А, нильпотентна, то есть ( А-Е п)n =0. Матрица над полем порядка пунипотентна тогда и только тогда, когда ее характеристический многочлен есть (x-1)n.
Группа матриц наз. унипотентной, если каждая ее матрица унипотентна. Любая унипотентная подгруппа в GL( п, F), где F - поле, сопряжена в GL(n,F )с нек-рой подгруппой специальной треугольной группы (теорема Колчина). Ото утверждение справедливо и для унипотентных групп над телом, если характеристика тела либо равна 0, либо больше нек-рого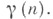
Д. А. Супруненко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
