- ТОЧЕЧНАЯ ОЦЕНКА
- статистическая оценка, значения к-рой суть точки во множестве значений оцениваемой величины.
Пусть по реализации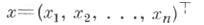
случайного вектора 
принимающего значения в выборочном пространстве 
надлежит оценить неизвестный параметр 
(или нек-рую функцию 
Тогда любая статистика Т n=Т п (Х), осуществляющая отображение множества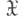 
в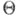 
(или в множество значений функции 
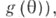наз. точечной оценкой параметра 
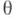(оцениваемой функции 
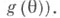Важными характеристиками Т. о. Т п являются ее математич. ожидание 
и дисперсионная матрица (ковариационная матрица)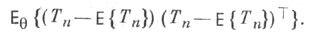
Вектор
наз. вектором ошибок Т. о. Т п. Если 
- нулевой вектор при всех
то говорят, что Т п является несмещенной оценкой функции 
или что Т п лишена систематич. ошибки, в противном случае Т. о. Т п наз. смещенной, а вектор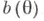 
- смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска. Лит.:[1] Крамер Г., Математические методы статистики, пер. с англ., 2изд., М., 1975; [2] Ибрагимов И. А., Хасьминский Р. 3., Асимптотическая теория оценивания, М., 1979.
М. С. Никулин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
