ТЕТРАЦИКЛИЧЕСКИЕ КООРДИНАТЫ
- ТЕТРАЦИКЛИЧЕСКИЕ КООРДИНАТЫ
точки на плоскости - четыре числа х 1, ,x2, х3, x4, подчиненные равенствам 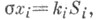 i=l, 2, 3, 4, где Si - степень точки относительно данных четырех окружностей, ki - произвольно заданные постоянные,
i=l, 2, 3, 4, где Si - степень точки относительно данных четырех окружностей, ki - произвольно заданные постоянные, 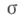 - множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду
- множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду 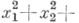
 если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы
если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы  i=1, 2, 3, и одна - мнимый
i=1, 2, 3, и одна - мнимый  а числа ki равными
а числа ki равными  Если в плоскости ввести декартовы координаты
Если в плоскости ввести декартовы координаты 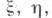 а в качестве трех действительных кругов взять
а в качестве трех действительных кругов взять  (круги, проходящие через бесконечно удаленную точку плоскости), круг
(круги, проходящие через бесконечно удаленную точку плоскости), круг 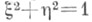 и мнимый круг
и мнимый круг  то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом:
то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом:
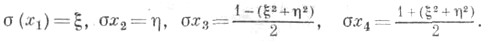
Можно ввести Т. к. и для круга на плоскости. При указанном специальном выборе четырех основных кругов круг с центром в точке 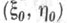 и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами
и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами

Т. к. точек и кругов на плоскости можно ввести с помощью стереографической проекции. При этом Т. к. точки на плоскости - однородные координаты соответствующей при стереографич. проектировании точки на сфере. Т. к. круга на плоскости - однородные координаты точки пространства, являющейся полюсом плоскости круга на сфере, соответствующего в стереографич. проекции кругу на плоскости, относительно этой сферы.
Обобщением Т. к. на случай трехмерного пространства являются пентасферические координаты.
Лит.:[1] Клейн Ф., Высшая геометрия, пер. с нем., М.-Л., 1939; [2] Бушманова Г. В., Норден А. II., Элементы конформной геометрии, Казань, 1972.
Г. В. Бушманова.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ТЕТРАЦИКЛИЧЕСКИЕ КООРДИНАТЫ" в других словарях:
Тетрациклические координаты — Тетрациклические координаты однородные координаты точки на плоскости, предложенные Дарбу[1]. Система тетрациклических координат задаётся четырьмя окружностями, а отношения координат точки выражаются уравнениями ( = 1, 2, 3, 4), где … … Википедия
Барицентрические координаты — У этого термина существуют и другие значения, см. Координаты. Барицентрические координаты координаты точки мерного аффинного пространства , отнесенные к некоторой фиксированной системе из ой точки , не лежащих в мерном подпространстве.… … Википедия
Параболические координаты — Параболические координаты ортогональная система координат на плоскости, в которой координатные линии являются конфокальными параболами. Трёхмерный вариант этой системы координат получается при вращении парабол вокруг их оси симметрии.… … Википедия
Биангулярные координаты — Биангулярные координаты система координат на плоскости с двумя фиксированными точками … Википедия
Биполярные координаты — Биполярная система координат … Википедия
Бицентрические координаты — Бицентрические координаты система координат на плоскости, в которой положение точки задаётся расстояниями от двух фиксированных центров (полюсов). Бицентрические координаты не следует путать с биполярными и с биангулярными координатами.… … Википедия
Трилинейные координаты — тесно связаны с барицентрическими координатами. А именно, если барицентрические координаты точки относительно треугольника , то её трилинейные координаты. Трилинейные координаты, как и барицентрические, определены с точностью до… … Википедия
Эллиптические координаты — Эллиптическая система координат Эллиптические координаты двумерная ортогональная система координат … Википедия
Цилиндрические параболические координаты — Координатные поверхности в координатах параболического цилиндра. Цилиндрические параболические координаты (координаты параболи … Википедия
Проективные координаты — Проективные координаты взаимно однозначное соответствие между элементами мерного проективного пространства над телом и классами эквивалентности упорядоченных конечных подмножеств элементов тела . Пусть в совокупности строк не равных… … Википедия
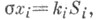 i=l, 2, 3, 4, где Si - степень точки относительно данных четырех окружностей, ki - произвольно заданные постоянные,
i=l, 2, 3, 4, где Si - степень точки относительно данных четырех окружностей, ki - произвольно заданные постоянные, 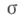 - множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду
- множитель пропорциональности. Т. к. связаны соотношением 2-й степени, к-рое приводится к виду 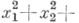
 если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы
если исходные окружности взять ортогональными (из них три обязательно имеют действительные радиусы  i=1, 2, 3, и одна - мнимый
i=1, 2, 3, и одна - мнимый  а числа ki равными
а числа ki равными  Если в плоскости ввести декартовы координаты
Если в плоскости ввести декартовы координаты 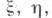 а в качестве трех действительных кругов взять
а в качестве трех действительных кругов взять  (круги, проходящие через бесконечно удаленную точку плоскости), круг
(круги, проходящие через бесконечно удаленную точку плоскости), круг 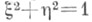 и мнимый круг
и мнимый круг  то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом:
то тогда Т. к. точки на плоскости выразятся через декартовы координаты следующим образом: 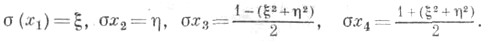
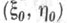 и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами
и радиусом R0 имеет Т. к. у i, i=1, 2, 3, 4, определенные формулами 
