ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ

- 1) Т. <п. унитарных модулей V₁ и V₂ над коммутативно-ассоциативным кольцом Ас единицей - A-модуль вместе с билинейным отображением

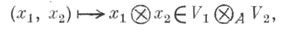
универсальным в следующем смысле: для любого билинейного отображения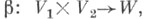 где W - произвольный A-модуль, существует единственное линейное отображение такое, что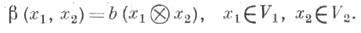

Т. п. определяется однозначно с точностью до изоморфизма. Оно всегда существует и может быть построено как фактормодуль свободного A-модуля F, порожденного множеством 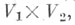по подмодулю R, порожденному элементами вида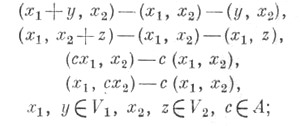

при этом 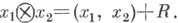Если отказаться от коммутативности кольца А, то близкая конструкция позволяет сопоставить правому A-модулю V₁ и левому А- модулю V₂ абелеву группу 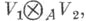также называемую Т. п. этих модулей [1]. В дальнейшем Апредполагается коммутативным.
Т. п. обладает следующими свойствами: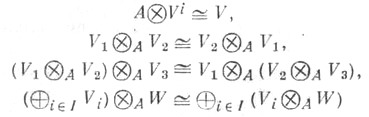

для любых А-модулей V, V_i, W.
Есл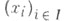и и - базисы модулей V₁ и V₂,то 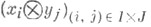- базис модуля В частности,

если V_i - свободные конечно порожденные модули (напр., конечномерные векторные пространства над полем А). Т. <н. циклич. A-модулей вычисляется по формуле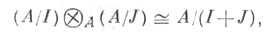
где I, J- идеалы в ..

Определяется также Т. п. любого (не обязательно конечного) семейства A-модулей. Т. п.

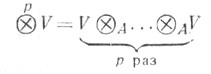
наз. р-й тензорной степенью A-модуля V;его элементы - это контравариантные тензоры валентности рна V.
Любым двум гомоморфизмам A-модулей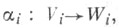 i=l, 2, сопоставляется их Т. <п. являющееся гомоморфизмом A-модулeй 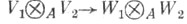и определяемое формулой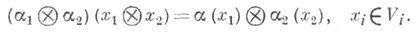

Эта операция также распространяется на любые семейства гомоморфизмов и обладает функторными свойствами (см. Модуль). Она определяет гомоморфизм A-модулей

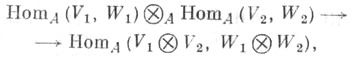
к-рый является изоморфизмом, если все V_i, W_i свободны и конечно порождены.

Лит.:[1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [2] Каш Ф., Модули и кольца, пер. с нем., М., 1981; [3] Костpикин А. И., Манин Ю. И., Линейная алгебра и геометрия, М., 1980.
А. Л. Онищик.

2) Т. п. алгебр С ₁ и С ₂ над коммутативно-ассоциативным кольцом . с единицей - алгебра над А, к-рая получается, если ввести в Т. п. А-модулей умножение по формуле

Определение распространяется на случай любого семейства сомножителей. Т. и. ассоциативно, коммутативно или содержит единицу, если этим свойством обладают обе алгебры С;. Если С ₁ и С ₂ - алгебры с единицами над полем А, то и -подалгебры в изоморфные С ₁ и С ₂ и поэлементно перестановочные. Обратно, пусть С - алгебра с единицей над полом А, С₁, С₂ - ееподалгебры, содержащие единицу и такие, что x₁x₂ = x₂x_l для любых Тогда существует гомоморфизм А-алгебр такой, что 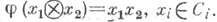Для того чтобы 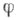был изоморфизмом, необходимо и достаточно, чтобы в Сосуществовал базис над А, являющийся базисом правого С ₂ -модуля С.

Лит.:[1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1062.
А. Л. Онищик.

3) Т. п., кронекерово произведение, матриц и В- матрица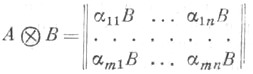

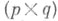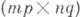Здесь Аесть -матрица, Весть -матрица, а есть -матрица над коммутативно-ассоциативным кольцом k с единицей. Свойства Т. п. матриц:

где

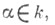
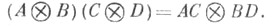
Если т=п и р = q, то

Пусть k - поле, т=п и р=q. Тогда подобна и где Е _п - единичная матрица, совпадает с результантом характеристич. многочленов матриц Аи В.
Если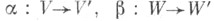 - гомоморфизмы унитарных свободных конечно порожденных k-модулей и А, В- их матрицы в нек-рых базисах, то является матрицей гомоморфизма 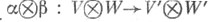в базисах, состоящих из Т. п. базисных векторов.

Лит.:[1] Халмош П., Конечномерные векторные пространства, пер. с англ., М., 1963; [2] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962, гл. 3.
Д. А. Супрупенко.

4) Т. п. представлений и группы Gв векторных пространствах E₁ и Е ₂ соответственно - представление группы G в векторном пространстве 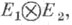однозначно определенное условием: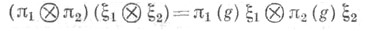

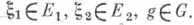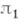для всех Если и - непрерывные унитарные представления топологич. группы Gв гильбертовых пространствах Е ₁ и Е ₂ соответственно, то операторы в векторном пространстве 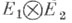допускают однозначное продолжение по непрерывности до непрерывных линейных операторов в гильбертовом пространстве 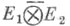(пополнении пространства относительно скалярного произведения, определяемого формулой 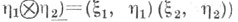и отображение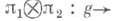 является непрерывным унитарным представлением группы Gв гильбертовом пространстве называемым тензорным произведением унитарных представлений и Представления 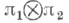и эквивалентны (унитарно, есл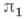и и 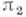унитарны). Операция Т. ц. может быть определена и для непрерывных представлений топологич. групп в топологич. векторных пространствах общего вида.

А. И. Штерн.

5) Т. п. векторных расслоений Еи Fнад топологическим пространством X - векторное расслоение 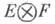над X, слоем к-poro в точке 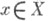является Т. п. слоев , Т. п. можно определить как расслоение, функции перехода к-рого являются Т. п. функций перехода расслоений Еи Fв одном и том же тривиализирующем покрытии (см. Тензорное произведение матриц).

Лит.:[1] Атья М., Лекции по К-теории, пер. с англ., М., 1967.
А. Л. Онищик.