- СТОКСА ФОРМУЛА
- 1) формула, выражающая связь между потоком векторного поля через двумерное ориентированное многообразие и циркуляцию этого поля по соответствующим образом ориентированному краю этого многообразия. Пусть S - ориентированная кусочно гладкая поверхность,
- единичная нормаль к поверхности S(в тех точках, конечно, где она существует), задающая ориентацию S, и пусть край поверхности Sсостоит из конечного числа кусочно гладких контуров. Через 
обозначен край поверхности S, ориентированный с помощью единичного касательного к нему вектора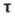 
так, чтобы получающаяся ориентация края 
была согласована с ориентацией v поверхности S.
Если а= ( Р, Q, R)- непрерывно дифференцируемое в окрестности поверхности Sвекторное поле, то
(dS - элемент площади поверхности S, ds - дифференциал длины дуги края
поверхности S)или, в координатном виде: 
Предложена Дж. Стоксом (G. Stokes, 1854). 2)С. ф. наз. также обобщение формулы (*), представляющее собой равенство интеграла от внешнего дифференциала дифференциальной формы
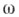по ориентированному компактному многообразию Ми интеграла от самой формы 
по ориентированному согласованно с ориентацией многообразия Мкраю 
многообразия М: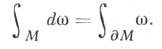 
Частными случаями этой формулы являются Ньютона - Лейбница формула, Грина формула, Остроградского формула.
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
